НИКОЛАЙ ИВАНОВИЧ ЛОБАЧЕВСКИЙ

(1792-1856)

С 14 лет жизнь Н.И.Лобачевского была связана с Казанским университетом. Его студенческие годы приходились на благополучный период в истории университета. Было у кого учиться математике; среди профессоров выделялся М.Ф. Бартельс, сотоварищ первых шагов в математике К. Ф. Гаусса.

С 1814 г. Лобачевский преподает в университете: читает лекции по математике, физике, астрономии, заведует обсерваторией, возглавляет библиотеку. В течение нескольких лет он избирался деканом физико-математического факультета.

С 1827 г. начинается 19-летний период его непрерывного ректорства. Все надо было начинать заново: заниматься строительством, привлекать новых профессоров, менять студенческий режим. На это уходило почти все время.

Еще в первых числах февраля 1826 г. он передал в университет рукопись «Сжатое изложение начал геометрии со строгим доказательством теоремы о параллельных», 11 февраля он выступил с докладом на заседании Совета университета. Собственно, речь шла не о доказательстве пятого постулата Евклида, а о построении геометрии, в которой имеет место его отрицание, т.е. о доказательстве его невыводимости из остальных аксиом. Вероятно, никто из присутствовавших не мог уследить за ходом мысли Лобачевского. Созданная комиссия из членов Совета несколько лет не давала заключения.

В 1830 г. в «Казанском вестнике» выходит работа «О началах геометрии», представляющая собой извлечение из доклада на Совете. Чтобы разобраться в ситуации, решили воспользоваться помощью столицы: в 1832 г. статью послали в Петербург. И здесь никто ничего не понял, работа была квалифицирована как бессмысленная. Не следует слишком сурово судить русских ученых: нигде в мире математики еще не были готовы воспринять идеи неевклидовой геометрии.

Ничто не могло поколебать уверенность Лобачевского в своей правоте. В течение 30 лет он продолжает развивать свою геометрию, пытается делать изложение более доступным, публикует работы по-французски и по-немецки.

Немецкую версию изложения прочитал Гаусс и, разумеется, понял автора с полуслова. Он прочитал его работы на русском языке и оценил их в письмах к ученикам, но публичной поддержки новой геометрии Гаусс не оказал.

Н. И. Лобачевский дослужился до высоких чинов, он был награжден большим числом орденов, пользовался уважением окружающих, но о его геометрии предпочитали не говорить, даже в те дни, когда Казань прощалась с ним. Прошло еще не менее двадцати лет, прежде чем геометрия Лобачевского завоевала права гражданства в математике.

------------------------------------------

Мы кратко коснулись только некоторых фактов геометрии Лобачевского, не упоминая многих других очень интересных и содержательных теорем (например, длина окружности и площадь круга радиуса r здесь растут в зависимости от r по показательному закону). Возникает убежденность, что эта теория, богатая очень интересными и содержательными фактами, в самом деле непротиворечива. Но эта убежденность (которая была у всех трех творцов неевклидовой геометрии) не заменяет доказательства непротиворечивости.

Чтобы получить такое доказательство, надо было построить модель. И Лобачевский это хорошо понимал и пытался ее найти.

Но сам Лобачевский этого уже не смог сделать. Построение такой модели (т.е. доказательство непротиворечивости геометрии Лобачевского) выпало на долю математиков следующего поколения.

В 1868 г. итальянский математик Э. Бельтрами исследовал вогнутую поверхность, называемую псевдосферой (рис. 10), и доказал, что на этой поверхности действует геометрия Лобачевского! Если на этой поверхности нарисовать кратчайшие линии («геодезические») и измерять по этим линиям расстояния, составлять из дуг этих линий треугольники и т.д., то оказывается, что в точности реализуются все формулы геометрии Лобачевского (в частности, сумма углов любого треугольника меньше 180°). Правда, на псевдосфере реализуется не вся плоскость Лобачевского, а лишь ее ограниченный кусок, но все же этим была пробита первая брешь в глухой стене непризнания Лобачевского. А через два года немецкий математик Ф. Клейн (1849-1925) предлагает другую модель плоскости Лобачевского.

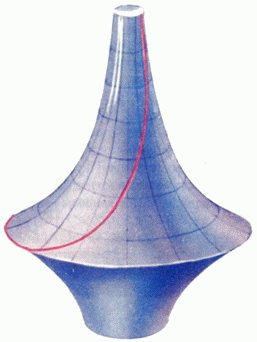
Рис. 10

Клейн берет некоторый круг K и рассматривает такие проективные преобразования плоскости (см. Проективная геометрия), которые отображают круг K на себя. «Плоскостью» Клейн называет внутренность круга K, а указанные проективные преобразования считает «движениями» этой «плоскости». Далее, каждую хорду круга K (без концов, поскольку берутся только внутренние точки круга) Клейн считает «прямой». Поскольку «движения» представляют собой проективные преобразования, «прямые» переходят при этих «движениях» в «прямые». Теперь в этой «плоскости» можно рассматривать отрезки, треугольники и т.д. Две фигуры называются «равными», если одна из них может быть переведена в другую некоторым «движением». Тем самым введены все понятия, упоминаемые в аксиомах геометрии, и можно производить проверку выполнения аксиом в этой модели. Например, очевидно, что через любые две точки A,B проходит единственная «прямая» (рис. 11). Можно проследить также, что через точку A, не принадлежащую «прямой» a, проходит бесконечно много «прямых», не пересекающих a. Дальнейшая проверка показывает, что в модели Клейна выполняются и все остальные аксиомы геометрии Лобачевского. В частности, для любой «прямой» l (т.е. хорды круга K) и любой точки A этой «прямой» существует «движение», переводящее ее в другую заданную прямую l' с отмеченной на ней точкой A'. Это и позволяет проверить выполнение всех аксиом геометрии Лобачевского.

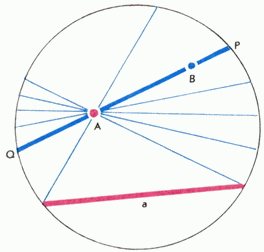
Рис. 11

Еще одна модель геометрии Лобачевского была предложена французским математиком А. Пуанкаре (1854-1912). Он также рассматривает внутренность некоторого круга K; «прямыми» он считает дуги окружностей, которые в точках пересечения с границей круга K касаются радиусов (рис. 12). Не говоря подробно о «движениях» в модели Пуанкаре (ими будут круговые преобразования, в частности инверсии относительно «прямых», переводящие круг K в себя), ограничимся указанием рис. 13, показывающего, что в этой модели евклидова аксиома параллельности места не имеет. Интересно, что в этой модели окружность (евклидова), расположенная внутри круга K, оказывается «окружностью» и в смысле геометрии Лобачевского; окружность, касающаяся границы Г круга K изображает орицикл, а дуга окружности, пересекающая Г (но не касающаяся радиусов), - эквидистанту. Заметим еще, что в геометрии Лобачевского правильный n-угольник может иметь любой угол при вершине, меньший 180°(1-2/n) (т.е. меньший аналогичного угла в евклидовой геометрии). Поэтому для любого n существует «паркет», представляющий собой замощение плоскости Лобачевского правильными n-угольниками (без пропусков и перекрытий). На рис. 14 приведен такой «паркет», изображенный в модели Пуанкаре (замощение плоскости Лобачевского правильными восьмиугольниками).

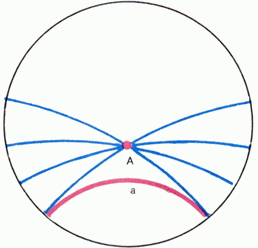
Рис. 12

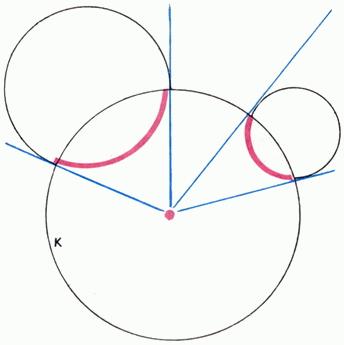
Рис. 13

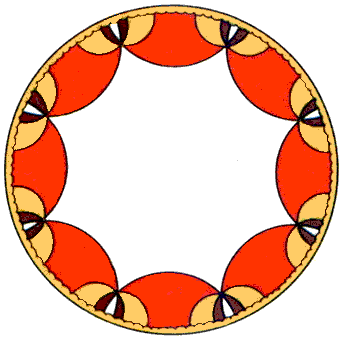
Рис. 14

Пуанкаре придумал фантастический мир, «жители» которого должны были бы принять геометрию Лобачевского из физических экспериментов. Для этого Пуанкаре предположил, что круг K представляет собой неоднородную оптическую среду, в которой скорость света в точке A∈K равна расстоянию точки A от границы круга K. Тогда свет будет (в соответствии с принципом Ферма о минимальности времени движения по световой траектории) распространяться как раз по «прямым» рассмотренной модели. Свет не может за конечное время дойти до границы (поскольку там его скорость убывает до нуля), и потому этот мир будет восприниматься его «жителями» бесконечным, причем по своей метрике и свойствам совпадающим с плоскостью Лобачевского.

Впоследствии были предложены и другие модели геометрии Лобачевского. Этими моделями была окончательно установлена непротиворечивость геометрии Лобачевского. Тем самым было показано, что геометрия Евклида не является единственно возможной. Это оказало большое прогрессивное воздействие на все дальнейшее развитие геометрии и математики в целом.

А в XX в. было обнаружено, что геометрия Лобачевского не только имеет важное значение для абстрактной математики, как одна из возможных геометрий, но и непосредственно связана с приложениями математики к физике. Оказалось, что взаимосвязь пространства и времени, открытая в работах X. Лоренца, А. Пуанкаре, А. Эйнштейна, Г. Минковского и описываемая в рамках специальной теории относительности, имеет непосредственное отношение к геометрии Лобачевского. Например, в расчетах современных синхрофазотронов используются формулы геометрии Лобачевского.