ПРОЕКЦИЯ

Проекцию фигуры (или тела) в пространстве можно представить себе как тень, отбрасываемую этой фигурой. За этим наглядным образом стоит несколько различных понятий: прямоугольная, или ортогональная, проекция, параллельная проекция, центральная проекция и др. Эти понятия широко используются в геометрии и других разделах математики, черчении, архитектуре и изобразительном искусстве, технике, географии, физике и астрономии. Не случайно и слово «проекция» и слово «проект» происходят от латинского слова projectio - «бросание вперед». Составляя описание будущего здания, сооружения, механизма - его проект, чертят план или общий вид - проекцию.

Определения разных видов проекций совпадают в одном: проекция фигуры - это множество проекций всех отдельных точек фигуры; при этом, конечно, разные точки могут проектироваться в одну.

В школьном курсе математики и в техническом черчении мы прежде всего встречаемся с прямоугольной проекцией. Пусть на плоскости задана прямая l. Проекцией точки M на прямую l называется основание M' перпендикуляра MM', проведенного из M к этой прямой. Например, проекцией круга на прямую в его плоскости будет всегда отрезок, равный по длине диаметру этого круга. Проекция на ось Ox точки (x,y) - это точка с координатой x; таким образом, проекцией графика функции y=f(x) на ось Ox служит область определения этой функции на ось Oy - множество ее значений (рис. 1,а). Проекция отрезка AB на ось Ox - отрезок длины  AB·cos α, а на оси Oy - отрезок длины AB·sin α, где α - величина угла между прямой AB и осью Ox (рис. 1,б).

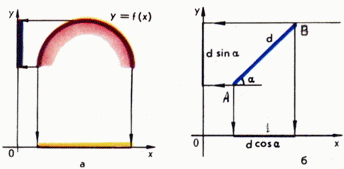
Рис. 1

Аналогично определяется прямоугольная (ортогональная) проекция в пространстве: проекция точки M на плоскость p - основание M' перпендикуляра 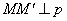. Площадь плоской фигуры при проектировании умножается на cos α, где α - величина угла между плоскостью фигуры и плоскостью ее проекции. Проекцией параллелепипеда на плоскость будет в общем случае шестиугольник (составленный из трех параллелограммов - проекций трех граней); в частном случае он может выродиться в параллелограмм. В одной из задач Московской математической олимпиады школьников спрашивалось: при каком положении прямоугольного параллелепипеда площадь его проекции на горизонтальную плоскость будет наибольшей? Для ее решения (рис. 2) достаточно сравнить площадь проекции S' с площадью треугольника A'B'C', являющегося проекцией сечения параллелепипеда плоскостью, проходящей через три несмежные вершины A,B,C:S' = 2S_A'B'C' и S_A'B'C' ≤ S_ABC, причем равенство достигается тогда, когда плоскость ABC горизонтальна: в этом положении площадь S' и будет наибольшей.

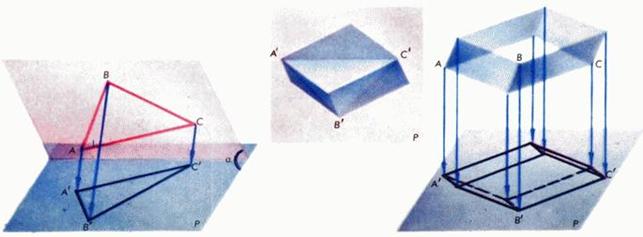
Рис. 2

Наряду с проекцией на плоскость можно говорить также о проекции на прямую l в пространстве. Ортогональная проекция точки M на прямую l - это точка M' пересечения l с плоскостью, проходящей через M и перпендикулярной l; например, проекция точки (x,y,z) пространства Oxyz на ось Oz - это точка на оси Oz с координатой z, а ее проекция на плоскость Oxy - точка с координатами (x,y). Аналогичная связь имеется между координатами вектора и координатами его проекций.

Прямоугольную проекцию тела на горизонтальную плоскость можно сравнить с его тенью от солнца, находящегося в зените. Если же солнце склоняется к горизонту, тень удлиняется. Эта тень и будет наклонной или параллельной проекцией на горизонтальную плоскость p по направлению α (α - прямая, задающая направление солнечных лучей); проекцией точки M при параллельной проекции по направлению α называется точка пересечения плоскости p с прямой, проходящей через M и параллельной α.

В технических чертежах часто приводят три проекции детали на взаимно ортогональные плоскости Ozy,Oyx,Oxz (рис. 3): вид спереди (анфас), вид сверху (план) и вид сбоку (профиль). Но для большей наглядности рядом помещают еще аксонометрическое изображение детали - ее параллельную проекцию на некоторую «наклонную» плоскость вместе с проекциями на эту плоскость трех осей Ox,Oy,Oz. Конечно, одна аксонометрическая проекция еще не задает формы тела и его расположения по отношению к осям координат, поэтому часто вместе с ней чертят также вторичную проекцию: аксонометрическое изображение одной из проекций тела и основных проецирующих лучей (на рис. 4 показана аксонометрия тела и его проекция на плоскость Oxy).

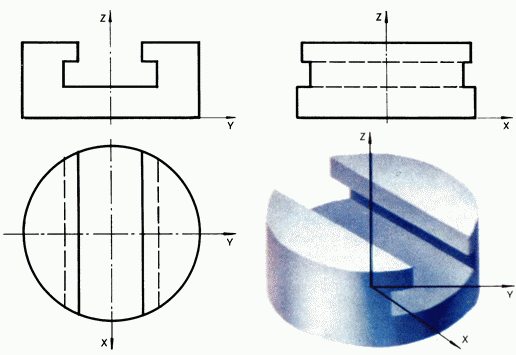
Рис. 3

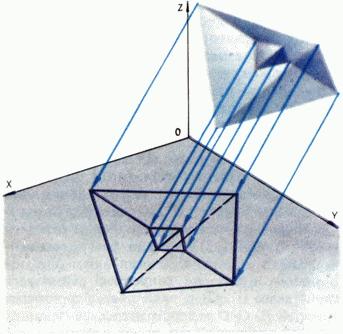
Рис. 4

При параллельной проекции, (разумеется, как и при ортогональной) искажаются углы между прямыми, но выполняются такие условия: (1) параллельные прямые переходят в параллельные прямые; (2) сохраняются отношения длин параллельных отрезков (и отрезков одной прямой); (3) площади фигур, расположенных в одной плоскости, уменьшаются в одном и том же отношении. Пользуясь свойствами (1), (2) и зная проекции четырех точек A,B,C,O в пространстве, не лежащих в одной плоскости (или, что то же самое, зная проекции трех непараллельных одной плоскости векторов 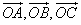), можно построить проекцию любой другой точки. При этом проекции A',B',C',O' могут занимать произвольные положения: для любого тетраэдра и любых четырех точек плоскости A',B',C',O' можно расположить в пространстве тетраэдр ABCO, подобный данному, вершины которого проецируются как раз в точки A',B',C',O'.

Этот факт называется теоремой Польке-Шварца, по именам немецких математиков К. Польке и Г. Шварца, доказавших ее в середине XIX в.

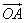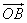Параллельная проекция плоскости на другую плоскость определяется образами O',A',B' трех точек O,A,B (двух векторов  и ); точка M, для которой 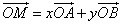, переходит в точку M', для которой 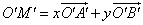. Свойства (1), (2), (3) показывают, что такая проекция - аффинное отображение одной плоскости на другую (и любое аффинное преобразование можно получить как композицию параллельных проекций (см. Геометрические преобразования).

Но свойства (1)-(3) уже не будут выполняться для центральной проекции. Центральной проекцией точки M с центром S на плоскость p называется точка M' пересечения прямой MS с плоскостью p. С этим видом проекции мы также сталкиваемся на каждом шагу. Тень от лампы, которую отбрасывает предмет на стену (рис. 5), - пример, когда фигура расположена между центром S и плоскостью проекции. Изображение в фотоаппарате (с некоторым приближением) - центральная проекция, центр которой расположен между предметом и плоскостью проекций p (изображение здесь получается перевернутым, рис. 6). Центральная проекция (ее также называют «линейная перспектива») играет большую роль и в изобразительном искусстве: скажем, рисуя на картине тень человека, отбрасываемую на асфальт от уличного фонаря, мы имеем дело с композицией двух центральных проекций: одна проекция человека с центром в лампочке фонаря на плоскость тротуара, вторая - проекция тени с центром в глазу художника на плоскость холста. Тут может спасти от ошибки лишь одно главное свойство центральной проекции: любую прямую она переводит в прямую. Изображением окружности при центральной проекции может быть не только эллипс (как при ортогональной или параллельной проекции), но также парабола или гипербола (рис. 7). Свойства фигур, сохраняющиеся при центральном проектировании, - предмет изучения проективной геометрии.

Рис. 5

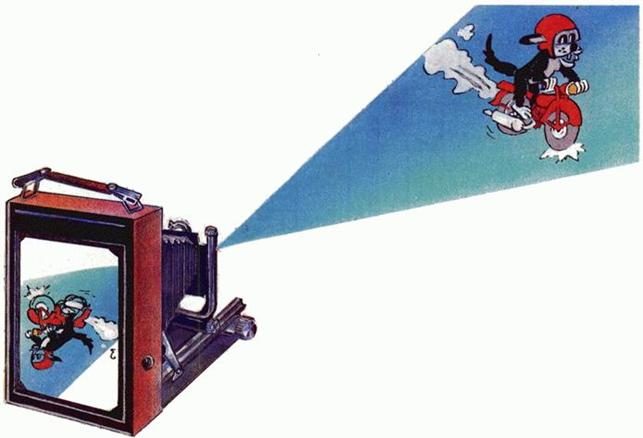
Рис. 6

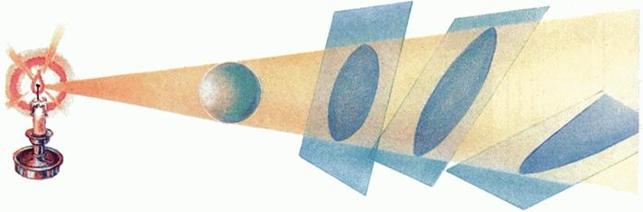
Рис. 7