ПАСКАЛЯ ТРЕУГОЛЬНИК

На рис. 1 изображено несколько первых строк числового треугольника, образованного по следующему правилу: по краям каждой строки стоят единицы, а каждое из остальных чисел равно сумме двух стоящих над ним чисел предыдущей строки. По этому правилу легко выписывать одну за другой новые строки этого треугольника. Именно в такой форме он приведен в «Трактате об арифметическом треугольнике» французского математика Б. Паскаля (1623-1662), опубликованном в 1665 г., уже после смерти автора. Но несколько иные варианты этой числовой таблицы встречались столетием раньше у итальянского математика Н. Тартальи, а за несколько веков до этого у среднеазиатского ученого и поэта Омара Хайяма, некоторых китайских и индийских ученых.

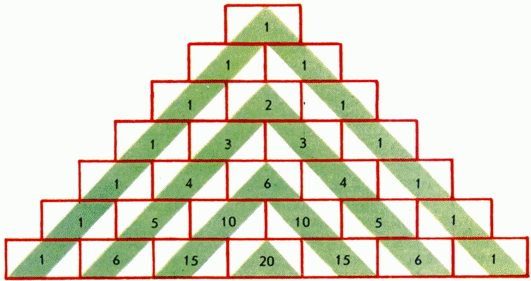
Рис. 1

Популярность чисел, составляющих треугольник Паскаля, не удивительна: они возникают в самых естественных задачах алгебры, комбинаторики, теории вероятностей, математического анализа, теории чисел.

Сколько различных k-элементных множеств (сочетаний) можно образовать из данных n элементов? (рис. 2).

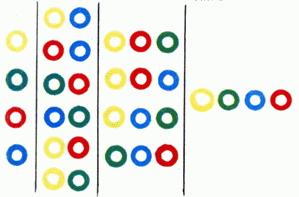
Рис. 2

Из 4 различных элементов можно составить такие множества 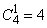 одноэлементных,  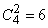двухэлементных,  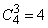трехэлементных и  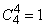четырехэлементное

Каковы коэффициенты многочлена (1+x)ⁿ?

Сколько существует строчек из n единиц и нулей, в которых ровно k единиц?

Сколькими разными путями можно спуститься из верхней точки A на рис. 3 в k-й перекресток n-го ряда?

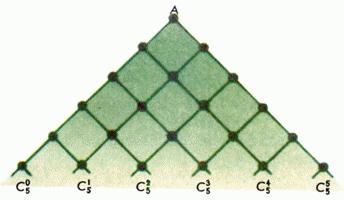
Рис. 3

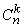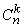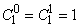На все эти вопросы ответ дают числа  треугольника Паскаля. Обозначение  предполагает, что верхняя строка треугольника Паскаля состоит из одного числа , следующая (первая) - из двух чисел , и вообще n-я строка состоит из n + 1 чисел:

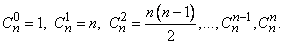
Числа 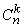 называют обычно числами сочетаний из n элементов по k, или биномиальными коэффициентами (см. Ньютона бином); в некоторых книгах для них используют обозначение 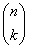. Оно удобно для запоминания простой формулы, позволяющей по заданным номерам n и k сразу вычислить, какое число стоит на k-м месте в n-й строке треугольника Паскаля:

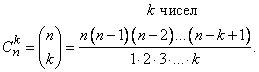
Используя обозначение факториала m! = 1·2·...·m, эту формулу можно записать еще короче:

.

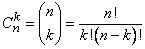В «равнобедренной» форме треугольника Паскаля на рис. 1 очевидно свойство симметрии каждой строки 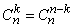; при этом посередине строки стоит самое большое число  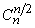(если n четно) или два самых больших числа  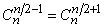(если n нечетно), а к краям числа монотонно убывают.

Если записать тот же треугольник в «прямоугольной» форме (рис. 4), то целый ряд свойств треугольника Паскаля, связанный с суммами его чисел, будет удобнее наблюдать. В частности, сумма нескольких первых чисел каждого столбца равна идущему за ними числу следующего столбца:

(числа 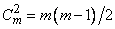 называются треугольными числами, а числа  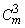- пирамидальными; см. Фигурные числа); и вообще, при m > k

.

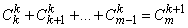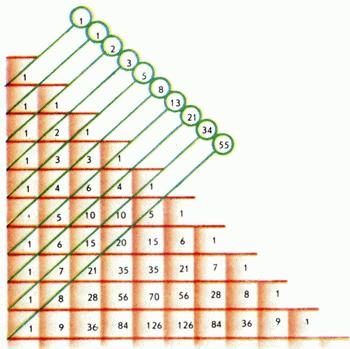
Рис. 4

Суммы чисел по «восходящим» (зеленым) диагоналям на рисунке 4 равны последовательным числам Фибоначчи (см. Фибоначчи числа).

Для применений в теории вероятностей особенно важны асимптотические формулы для чисел треугольника Паскаля, т.е. приближенные оценки этих чисел при больших n.