НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ
Наименьшее натуральное число, делящееся на каждое из данных целых чисел, называется наименьшим общим кратным этих чисел. Для чисел a1,a2,...,an оно обозначается [a1,a2,...,an] Например: [4,6]=12, [21,42,63]=126. Если числа a и b одного знака, то [a,b]=ab/(a,b), где (a,b)- наибольший общий делитель чисел a и b. Таким образом, вычисление наименьшего общего кратного чисел можно свести к вычислению их наибольшего общего делителя. Если же нам известны разложения чисел a и b на простые множители, то получить наименьшее общее кратное чисел a и b можно так: выписать подряд простые числа, входящие хотя бы в одно из разложений, причем если простое число p входит k раз в разложение одного из чисел, l раз в разложение другого и k<l, то число p следует выписать l раз; произведение всех выписанных чисел и даст наименьшее общее кратное чисел a и b.
Пример. Найдем [100,150 и 108]:
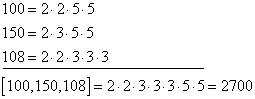
При сложении дробей мы обычно приводим их к общему знаменателю, который является наименьшим общим кратным знаменателей данных дробей.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК