АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ

Арифметической прогрессией называют последовательность (a_n), у которой каждый член, начиная со второго, больше (или меньше) предыдущего на постоянное (для данной прогрессии) число d. Число d называют разностью арифметической прогрессии. Другими словами, арифметическая прогрессия – это последовательность, заданная по правилу: a₁ и d даны, a_n+1 = a_n + d при n ≥ 1.

Каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому последующего и предыдущего членов:

.

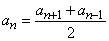Это отражено в названии последовательности: арифметическая прогрессия. Верно и более общее свойство:

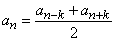 при n≥k.

Справедливы следующие формулы (через S_n обозначена сумма первых n членов арифметической прогрессии):

a_n = a₁ + (n-1)d,   (1)

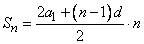,   (2)

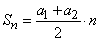. (3)

С формулой (3) связан интересный эпизод из жизни немецкого математика К.Ф. Гаусса (1777-1855). Когда ему было 9 лет, учитель, занятый проверкой работ учеников других классов, задал на уроке следующую задачу: «Сосчитать сумму всех натуральных чисел от 1 до 40 включительно:

1+2+3+4+5+...+40».

Каково же было удивление учителя, когда один из учеников (это был Гаусс) через минуту воскликнул: «Я уже решил». Большинство учеников после долгих подсчетов получили неверный результат. В тетради Гаусса было только одно число, но зато верное.

Вот схема его рассуждений. Сумма чисел в каждой паре равна 41:

1, 2, 3, ... , 20

+

40, 39, 38, ..., 21

------------------

41, 41, 41, ..., 41

Таких пар 20, поэтому искомая сумма равна 41·20 = 820.

Арифметические прогрессии и их свойства изучались математиками с древних времен. Греческих математиков интересовала связь прогрессий с так называемыми многоугольными числами (см. Фигурные числа), вычислением площадей, объемов, красивыми числовыми соотношениями типа:

1 = 1²

1 + 3 = 2²

1 + 3 + 5 = 3²

1 + 3 + 5 + 7= 4²

1 = 1³

3 + 5 = 2³

7 + 9 + 11 = 3³

13 + 15 + 17 + 19 = 4³

Большой популярностью даже в наши дни пользуются магические квадраты (см. Магические и латинские квадраты). Это квадраты, в каждую клетку которых вписаны числа так, что суммы чисел вдоль любой горизонтали, любой вертикали и любой диагонали равны (рис. 1). Такой магический квадрат изображен на гравюре немецкого художника А. Дюрера «Меланхолия».

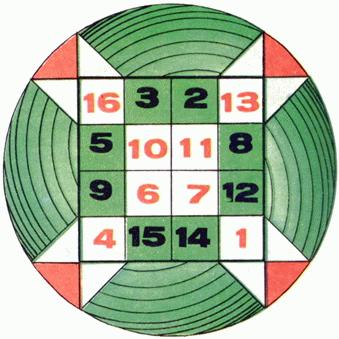
Рис. 1