КЛАССИЧЕСКИЕ ЗАДАЧИ ДРЕВНОСТИ

Древнегреческие математики достигли чрезвычайно большого искусства в геометрических построениях с помощью циркуля и линейки. Однако три задачи не поддавались их усилиям. Прошли тысячелетия, и только в наше время, наконец, были получены их решения.

Вот эти задачи: построение квадрата, равновеликого данному кругу (или, сокращенно, квадратура круга); деление произвольно заданного угла или дуги на три равновеликие части (или трисекция угла), и построение куба, объем которого вдвое больше объема заданного куба (или удвоение куба).

История нахождения квадратуры круга длилась четыре тысячелетия, а сам термин стал синонимом неразрешимых задач. Как следует из подобия кругов, отношение длины окружности к ее диаметру есть величина постоянная, не зависящая от радиуса круга, она обозначается буквой π. Таким образом, длина окружности круга радиуса r равна 2πr, а так как площадь круга равна S = πr² (см. Окружность и круг), то задача о квадратуре круга сводится к задаче построения треугольника с основанием 2πr и высотой r. Для него потом уже без труда может быть построен равновеликий квадрат (см. Равновеликие и равносоставленные фигуры).

Итак, задача сводилась к построению отрезка, длина которого равна длине окружности данного круга. Это было показано еще Архимедом в сочинении «Измерение круга», где он доказывает, что число π меньше чем 3 1/7, но больше чем 3 10/71, т.е. 3,1408 < π < 3,1429.

В наши дни с помощью ЭВМ число π вычислено с точностью до миллиона знаков, что представляет скорее технический, чем научный интерес, потому что такая точность никому не нужна. Десяти знаков числа π ( π = 3,141592653...) вполне достаточно для всех практических целей. Долгое время в качестве приближенного значения π использовали число 22/7, хотя уже в V в. в Китае было найдено приближение 355/113 = 3,1415929..., которое было открыто вновь в Европе лишь в XVI в. В Древней Индии π считали равным √10 = 3,1622.... Французский математик Ф. Виет вычислил в 1579 г. π с 9 знаками. Голландский математик Лудольф Ван Цейлен в 1596 г. публикует результат своего десятилетнего труда - число π, вычисленное с 32 знаками.

Но все эти уточнения значения числа  производились методами, указанными еще Архимедом: окружность заменялась многоугольником со все большим числом сторон (рис. 1,а). Периметр вписанного многоугольника при этом был меньше длины окружности, а периметр описанного многоугольника - больше. Но при этом оставалось неясным, является ли число π рациональным, т.е. отношением двух целых чисел, или иррациональным. Лишь в 1767 г. немецкий математик И. Г. Ламберт доказал, что число π иррационально, а еще через сто с лишним лет в 1882 г. другой немецкий математик - Ф. Линдеман доказал его трансцендентность (см. Число), что означало и невозможность построения при помощи циркуля и линейки квадрата, равновеликого данному кругу.

«Возьму линейку, проведу прямую. И мигом круг квадратом обернется». Аристофан

Конечно, способов приближенного решения квадратуры круга с помощью циркуля и линейки было придумано великое множество. Так, в Древнем Египте было распространено правило: площадь круга равна площади квадрата со стороной, равной 8/9; π = 256/81 = 3,1604....

Были найдены и другие пути определения квадратуры круга: кроме циркуля и линейки использовали другие инструменты или специально построенные кривые. Так, в V в. до н. э. греческий математик Гиппий из Элиды изобрел кривую, впоследствии получившую название квадратрисы Динострата (ее назвали по имени другого древнегреческого математика, жившего несколько позже и указавшего способ построения квадратуры круга при помощи этой кривой).

Квадратриса Динострата получается следующим образом. Пусть дана окружность радиуса a (рис. 1,б). Начнем вращать радиус OA с угловой скоростью π/2 вокруг точки O - центра окружности - и одновременно равномерно перемещать влево со скоростью a вертикальную прямую от точки A к точке C. Точка M их пересечения и будет описывать квадратрису. Если взять за оси координат прямую OA и прямую OB, то в момент времени t точка M будет иметь координаты

a(1-t) и a(1-t) tg πt/2.

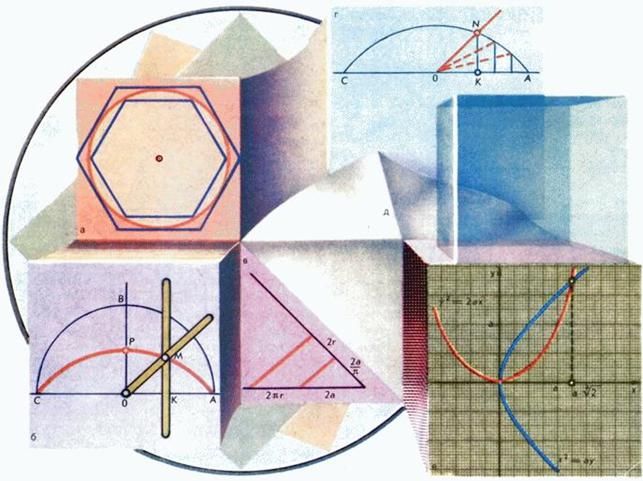
Рис. 1

При стремлении t к 1 точка M стремится к точке P, при этом абсцисса точки M стремится к нулю, а у ординаты один множитель стремится к нулю, а другой – к бесконечности. Их произведение будет стремиться к числу 2a/π, поэтому длина отрезка OP равна 2a/π. Следовательно, имеет место соотношение AC/OP = π.

Пусть теперь дана окружность радиуса r. Тогда имеем соотношение 2πr/2r = AC/OP, в котором известны AC, OP и 2r - диаметр данной окружности. По ним мы можем построить отрезок, равный 2πr - длине окружности, это будет четвертый пропорциональный отрезок к известным трем (рис. 1,в).

Чрезвычайно любопытно, что квадратриса Динострата решает и вторую из знаменитых задач древности – задачу о трисекции угла. Для этого нужно отложить данный угол так, чтобы его вершина находилась в точке O, а одна из сторон совпала с лучом OA (рис. 1,г). Из точки N пересечения квадратрисы со вторым лучом угла опускаем перпендикуляр NK на OA, а затем делим отрезок KA на три равные части. Если восставить в точках деления перпендикуляры к прямой OA до пересечения с квадратрисой, а затем соединить полученные точки пересечения с точкой O, то полученные углы окажутся равными. Это следует из метода построения квадратрисы. Аналогичным образом можно делить любой угол на произвольное количество равных частей.

Напомним, что в классической постановке задачи о трисекции угла такое построение требовалось произвести лишь с помощью циркуля и линейки! В 1837 г. французский математик П. Ванцель доказал, что в общем виде задача не имеет решения, а возможно такое деление лишь в нескольких исключительных случаях, в частности для угла α = π/2 и всех углов вида π/2ⁿ.

Как известно, имеет место тождество cos α = 4 cos³ α/3 - 3 cos α/3. Если обозначим 2 cos α = a, 2 cos α/3 = x, то получим такое кубическое уравнение: x³ - 3x - a = 0. Оказалось, что трисекция угла возможна для тех углов α, для которых корни этого уравнения выражаются через параметр a и целые числа лишь с помощью операций сложения, вычитания, умножения, деления и извлечения квадратного корня. В частности, если α = π/2, т. е. a = 0, то получаем уравнение x³ - 3x = 0, имеющее корни 0, +√3, -√3.

К кубическому уравнению сводится и знаменитая «делосская задача» удвоения куба. Свое название она получила от острова Делос в Эгейском море, где, по легенде, чтобы избавить жителей от эпидемии, оракул повелел удвоить алтарь, имевший форму куба. Но в действительности она, наверное, возникла в умах математиков как обобщение задачи об удвоении квадрата. Для того чтобы построить квадрат вдвое большей площади, чем данный, достаточно провести у данного квадрата диагональ (рис. 1,д) и принять ее за сторону нового квадрата.

Задача об удвоении куба оказалась существенно более трудной. Если обозначить через a длину стороны исходного куба, а через x – длину стороны вдвое большего куба, то получим соотношение x³ = 2a³ – снова кубическое уравнение. В 1837 г. тот же П. Ванцель доказал, что невозможно построить с помощью только циркуля и линейки отрезок, в 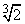 раз больший данного, т.е. подтвердил неразрешимость задачи удвоения куба.

Естественно, что существовали способы приближенного решения этой задачи и решения ее с помощью других инструментов и кривых. Так, уже в IV в. до н.э. древнегреческие математики умели находить корень уравнения x³ = 2a³ как абсциссу точки пересечения двух парабол x² = ay и y² = 2ax (рис. 1,е), а также других конических сечений.

На протяжении многих веков три знаменитые задачи древности привлекали внимание выдающихся математиков. В процессе их решения рождались и совершенствовались многие математические методы.