КУБ

Куб, или гексаэдр (шестигранник), - прямоугольный параллелепипед с равными измерениями, один из видов правильных многогранников. Ею легко склеить из развертки (рис. 1). Куб – единственный из правильных многогранников, которым можно замостить пространство, прикладывая один кубик к другому. Именно поэтому объем куба с единичным ребром принят за единицу объема. Удивительным образом куб связан с четырьмя другими видами правильных многогранников. Так, центры граней куба являются вершинами октаэдра и, наоборот, центры граней октаэдра суть вершины куба (рис. 2).

Рис. 1

Рис. 2

В куб можно вписать правильный тетраэдр – его вершинами являются концы скрещивающихся диагоналей двух параллельных граней куба (рис. 3). Остальные четыре вершины куба служат вершинами второго вписанного тетраэдра.

Рис. 3

Куб можно вписать в додекаэдр так, что ребра куба будут диагоналями граней додекаэдра (рис. 4). Ребром вписанного в додекаэдр куба может быть любая из пяти диагоналей какой-нибудь грани додекаэдра, так что в додекаэдр указанным образом можно вписать 5 одинаковых кубов. Наконец, на каждой из шести граней куба можно выбрать по паре точек так, что 12 выбранных точек будут вершинами икосаэдра, рис. 5 (выделенные отрезки лежат на гранях куба).

Рис. 4

Рис. 5

Среди прочих примечательных свойств куба отметим, что в точности четыре его сечения являются правильными шестиугольниками – эти сечения проходят через центр куба перпендикулярно четырем его диагоналям (рис. 6).

Рис. 6

Куб – пространственный аналог квадрата на плоскости. Особую четкость эта аналогия приобретает, если привлечь координаты. Квадрат на плоскости Oxy можно задать неравенствами

0≤x≤1, 0≤y≤1,

и его вершины будут иметь координаты (0;0), (0;1), (1;0) и (1;1). В координатном пространстве Oxyz куб задается неравенствами

0≤x≤1, 0≤y≤1, 0≤z≤1;

его 8 вершин имеют координаты (0;0;0), (0;0;1), (0;1;0), (0;1;1), (1;0;0), (1;0;1), (1;1;0) и (1;1;1). Квадрат имеет 4 стороны, лежащие на прямых x=0, y=0, x=1 и y=1. Куб имеет 6 (плоских, или двумерных) граней, лежащих в плоскостях, задаваемых уравнениями x=0, y=0, z=0, x=1, y=1 и z=1. Эту аналогию можно продолжить в две стороны.

Одномерный аналог куба и квадрата – это, конечно, отрезок 0≤x≤1 оси Ox. Четырехмерный же куб в четырехмерном пространстве, точки которого понимают как всевозможные (упорядоченные) четверки чисел (x;y;z;t), задается системой неравенств

0≤x≤1, 0≤y≤1, 0≤z≤1, 0≤t≤1.

Четырехмерный куб, или гиперкуб, имеет уже 16 вершин (точек с координатами (x;y;z;t), где x,y,z и t могут равняться 0 или 1) и 8 трехмерных граней, каждая из которых представляет собой обычный (трехмерный) куб, все 8 вершин которого удовлетворяют одному из уравнений: x=0, y=0, z=0, t=0, x=1, y=1, z=1 и t=1. Двумерных граней у гиперкуба 24 – это квадраты, у вершин которых зафиксированы (равны 0 или 1) уже две координаты (из четырех). Наконец, ребер, одномерных граней, у гиперкуба 32.

Аналогично тому, как обычный куб имеет плоскую – двумерную – развертку (рис. 1), гиперкуб может быть «развернут» в трехмерном пространстве. Эта развертка будет состоять из 8 трехмерных граней – обычных кубов – и может быть изображена так, как показано на рис. 7. В четырехмерном пространстве каждый из кубов развертки граничит с шестью другими. На рис. 8 дан плоский чертеж трехмерного «изображения» гиперкуба (само это изображение легко соорудить из спичек и пластилина). Пространственную проекцию гиперкуба можно представить и изготовить по плоскому чертежу на рис. 9.

Рис. 7

Рис. 8

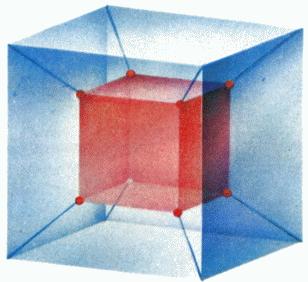
Рис. 9