СИНУСОВ ТЕОРЕМА

Эта теорема устанавливает зависимость между сторонами треугольника и противолежащими им углами. Она утверждает, что длины a, b, c сторон любого треугольника ABC (см. рис. 1) пропорциональны синусам противолежащих углов, т.е.

a/sin A = b/sin B = c/sin C = 2R,

где R - радиус описанной окружности.

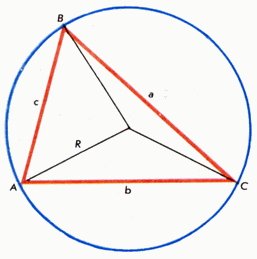
Рис. 1

Подчеркнем, что стороны треугольника пропорциональны лишь синусам его внутренних углов, но не пропорциональны самим углам. Так, в прямоугольном треугольнике с острыми углами 30° и 60° sin 90° больше sin 30° в 2 раза: 1:1/2 = 2, гипотенуза больше катета, лежащего против угла 30°, также в 2 раза. Но угол 90° больше угла 30° в 3 раза.

По теореме синусов удобно вычислять длины сторон треугольника, если известны величины его углов и длина одной из сторон.

Теорема синусов была впервые доказана в X-XI вв. математиками Ближнего и Среднего Востока. Открытие этой теоремы сыграло важнейшую роль в развитии тригонометрии.