ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ

Эта функция представляет собой частное двух линейных функций и задается формулой:

y = (ax + b) / (cx + d).   (1)

Дробно-линейная функция сводится к линейной функции при c=0 и к постоянной при ad=bc.

Особенно важен частный случай дробно-линейной функции при a=d=0, так как он выражает закон обратной пропорциональной зависимости:

y = k/x.   (2)

Обратная пропорциональная зависимость связывает, например, давление газа p и его объем v при постоянной температуре, так как по закону Бойля-Мариотта pv = const. В случае равномерного движения при прохождении заданного пути s время движения t обратно пропорционально скорости v, т.е. t=s/v.

Графики функций y=k/x при различных значениях k изображены на рис. 1: сплошной линией при k>0 и пунктирной при k<0. Все эти кривые называются равнобочными гиперболами, они стремятся к оси Ox при неограниченном возрастании и убывании аргумента x и стремятся к оси Oy при стремлении x слева или справа к нулю.

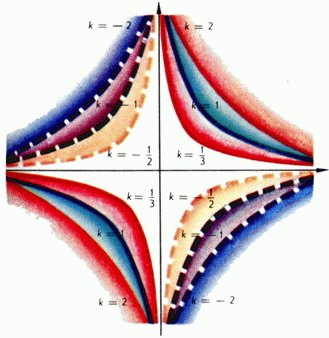
Рис. 1

График общей дробно-линейной функции (1) получается из графика функции y=k/x при помощи параллельного переноса. На рис. 2 приведен график функции

y = (2x + 3) / (x - 1).

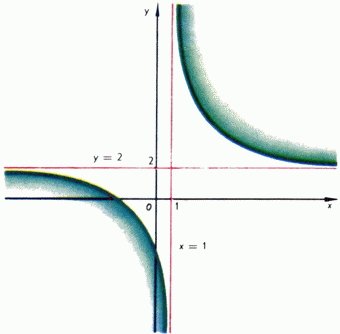
Рис. 2

Эта функция представима в виде

y = 2 + 5 / (x - 1),

и легко понять, что ее график получается параллельным переносом из равнобочной гиперболы y=5/x и заключен между прямыми x=1 и y=2, к которым неограниченно приближается.