2.3. Задачи на пропорциональные отрезки

Теорема Фалеса (а также теоремы Чевы и Менелая) применяются в первую очередь тогда, когда в задаче даны соотношения между отрезками. Очень часто при этом приходится проводить дополнительный отрезок. Идеи использования теоремы Фалеса хорошо видны на следующих примерах.

Примеры решения задач

102. Докажите, что медианы в треугольнике делятся в отношении 2:1, считая от вершины (известная теорема школьного курса математики). (2)

Самый простой путь решения (рис. 173):

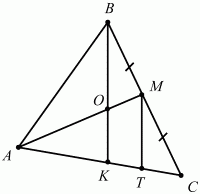
Рис. 173.

Проведем медианы AM и ВК, а также отрезок МТ, параллельный ВК. Имеем: т. к. ВМ = МС, то КТ = ТС. Но тогда АК = КС = 2КТ и, значит, АО: ОМ = АК: КТ = 2, что и требовалось доказать.

103. В треугольнике ABC на стороне ВС взята точка М так, что MB = МС, а на стороне АС взята точка К так, что АК = 3 ? КС. Отрезки ВК и АМ пересекаются в точке О. Найдите AO/OM (рис. 174). (2)

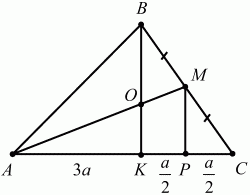
Рис. 174.

Решение. Обозначим длину отрезка КС через а, тогда АК = За. Проведём MP||ВК По теореме Фалеса КР = РС = a/2. По теореме о пропорциональных отрезках имеем:

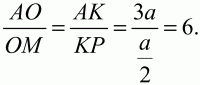
Ответ: 6.

104. В треугольнике ABC на стороне АВ взята точка К так, что АК: ВК = 1:2, а на стороне ВС взята точка L так, что CL: BL = 2:1. Пусть Q – точка пересечения прямых AL и СК. Найти площадь треугольника ABC, если дано, что площадь треугольника BQC равна 1 (рис. 175). (3)

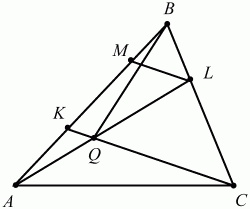
Рис. 175.

Решение. Проведём через точку L прямую LM параллельно прямой СК. Из подобия треугольников MBL и КВС следует, что

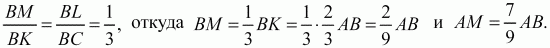
Из подобия треугольников AKQ и AML находим:

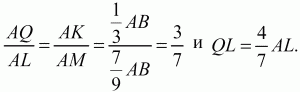
Кроме того, имеем следующие равенства:

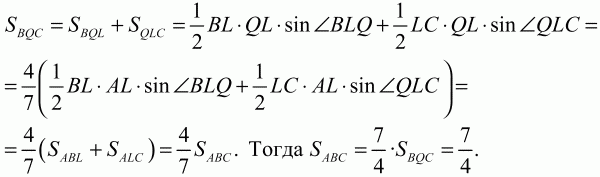
Ответ: 7/4.

Задачи для самостоятельной работы

105. ВМ: МС = 3:1, АК = КВ. Найдите: SAKO/SABC(рис. 176). (2)

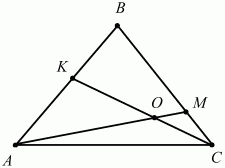
Рис. 176.

106. На сторонах АВ и АС треугольника ABC взяты точки M и N, такие, что AM/MB = CN/NA = 1/2.

Отрезки BN и СМ пересекаются в точке К. Найти отношения отрезков BK/KN и CK/KM.(2)