Задача 26 (рис. 230)
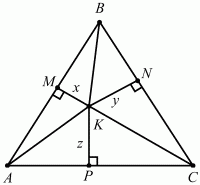
Рис. 230.
Решение. Пусть К – произвольная точка внутри равностороннего треугольника ABC со стороной а. Опустим перпендикуляры KM, KN, КР на стороны треугольника. Обозначим эти перпендикуляры следующим образом: КМ = х, KN = у, КР = z. Тогда SABC = SABK + SBKC + SAKC. Получаем равенство:
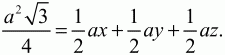
Отсюда (a?3)/2 = x + y + z. Но высота h треугольника равна h = a ? sin 60° = (a?3)/2; значит, х + у + z = h.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК
Содержание
История
История
Loading ...
Failed to load data.
{{name}} | {{author}}