Задача 66 (рис. 253)
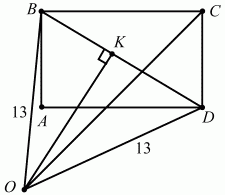
Рис. 253.
Решение. Для определённости будем считать, что АВ < AD. Так как AB ? AD = 48 и АВ2+ AD2= BD2= 100, то AD = 8, АВ = 6. Поскольку OB = OD = 13 > BD, то точка О лежит вне круга с диаметром BD и потому вне прямоугольника. Пусть она находится по ту же сторону от диагонали BD, что и точка А. Тогда требуется найти ОС. Обозначим ?OBD через ? и ?DВС через ?. Чтобы найти угол ?, опустим из точки О на диагональ BD перпендикуляр ОК. Получим ВК = KD = 1/2BD. Из прямоугольного ?ОВК следует:
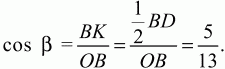
Тогда sin ? = 12/13. Из прямоугольного ?DBС находим:
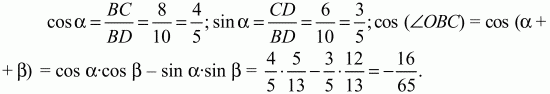
Применяя к треугольнику OBС теорему косинусов, получаем
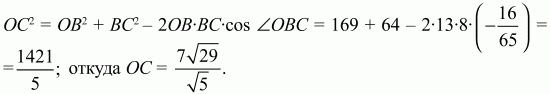
Ответ:
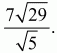
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК
Содержание