Ответы и указания к задачам экзаменационного комплекта № 1
Билет № 1
3) 74°.
4) ?1/?2 = R2/R1.
Билет № 2
3) 94 см.
4) AB + BD + DC = 14 см.
Билет № 3
3) 12? см2.
4) Воспользоваться тем, что две крайние части средней линии трапеции равны половине верхнего основания.
Билет № 4
3) 4 и 6 см.
4) Если В1К1С – точки касания (К – точка касания окружностей), О1, О2 – центры окружностей, то сначала доказываем, что ?АО1К = ?АКO2, а затем, что ?ВАО1 = ?АO2С.
Билет № 5
3) 5 см (воспользоваться подобием ?DCE и ?АСЕ).
4) Воспользоваться теоремой Фалеса.
Билет № 6
3) Воспользуйтесь свойством параллельных прямых.
4) Учесть то, что треугольник разбивается на прямоугольник и два равнобедренных треугольника (значит, сторона прямоугольника равна катету малого треугольника). Периметр равен сумме катетов.
Билет № 7
3) 12 см (?BOF ~ ?AOD).
4) Докажите, что расстояния от точки пересечения диагоналей до сторон ромба равны.
Билет № 8
3) Докажите равенство углов DBA и ACF и воспользуйтесь признаком параллельности прямых.
4) Выразите по теореме Пифагора квадрат каждой стороны четырёхугольника через соответствующие отрезки диагоналей.
Билет № 9
3) 68°, 68° и 44°.
4) 4?3 см и 6?2 см.
Билет № 10
3) 4 (т. к. 180° (n – 2) = 360°).
4) Если АС = а, то AD = a/2, АВ = 2а, DB = 3a/2.
Билет № 11
3) 56 см.
4) В равностороннем треугольнике биссектрисы и медианы совпадают; воспользуйтесь свойством точки пересечения медиан.
Билет № 12
3) 66° и 66°.
4) По 60°.
Билет № 13
3) 8, 6 и 6 см.
4) 60° (угол DOG, больший 180°, равен 2 ? 150° = 300°).
Билет № 14
3) 13 см.
4) Стороны равностороннего треугольника – по 12 см, а равнобедренного – 12, 14 и 14 см.
Билет № 15
3) Треугольники равны по двум сторонам и углу между ними.
4)
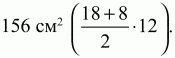
Билет № 16
3) Треугольники равны по двум сторонам и углу между ними.
4) 1:1:?3.
Билет № 17
3) 5 см (обозначьте АВ = ВС = a; AD = DC = в, BD = х и запишите систему уравнений).
4) 12 и 8 см (докажите равенство ?AMP и ?PNC, из которого следует, что АР = 12).
Билет № 18
3) 67°.
4) Воспользуйтесь тем, что внешний угол треугольника равен сумме двух внутренних, с ним не смежных.
Билет № 19
3) 25/2 см2.
4) 5 (т. к. сумма внешних углов равна 360°, то угол в правильном многоугольнике равен 468° – 360° = 108°. Далее: 180°(n – 2)/n = 108°; n = 5).
Билет № 20
3) Пусть АВ – общая хорда двух окружностей с центрами О1 и O2, ?О1АO2 = ?О1BO2 (по трем сторонам), значит, углы АO2О1 и O1O2B равны, а биссектриса в равнобедренном треугольнике является и высотой.
4) 16 (т. к. в трапецию вписана окружность, то сумма оснований – а она равна 8 – равна сумме боковых сторон).
Билет № 21
3) Увеличивается на 20? см.
4) Проведите диагонали в трапеции, рассмотрите средние линии полученных треугольников и учтите равенство боковых сторон трапеции.
Билет № 22
3) С(0; -6).
4) 20 см.
Билет № 23
3) Медиана в равнобедренном треугольнике является и серединным перпендикуляром.
4) Окружность (середины равных хорд окружности равноудалены от центра окружности).