Задача 122 (рис. 283)

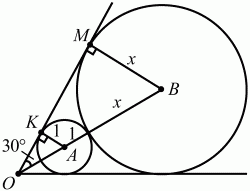
Рис. 283.

Решение. Обозначим радиус большей окружности через х. Из рисунка видно, что из прямоугольного треугольника ОКА ОА = AK/sin 30° = 1/(1/2) = 2. Треугольники OAK и ОВМ подобны, поэтому ОА/OB = АК/BM; 2/(3 + x) = 1/x; 2х = 3 + х; х = 3.

Ответ: 3.