Задача 156 (рис. 301)

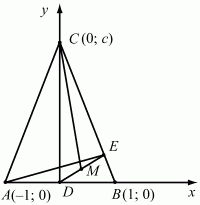
Рис. 301.

Решение. Высота равнобедренного треугольника является его осью симметрии. Поэтому середину D основания АВ треугольника ABC удобно принять за начало прямоугольной системы координат, а направленные прямые АВ и DC – за оси координат. Тогда вершинам треугольника можно отнести координаты: А(-1; 0), B(1; 0), С(0; с).

Вычислим угловые коэффициенты прямых АЕ и СМ. Для этого сначала найдём координаты точек Е и М. Запишем уравнение прямой ВС: х + у/с = 1 или у = – сх + с.

Так как DE ? ВС, то угловой коэффициент прямой DE равен 1/с, а её уравнение есть у = (1/c)x. Решая систему уравнений

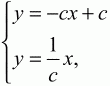
находим координаты точки Е:

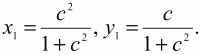
Следовательно, М (х1/2; у1/2).

Угловые коэффициенты прямых АЕ и СМ равны соответственно

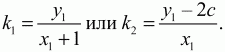
Подставив значения x1 и у1 получим:

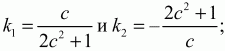
k1k2 = -1, что говорит о перпендикулярности прямых. Значит, отрезки АЕ и СМ перпендикулярны.