2.4. Задачи на свойства биссектрисы треугольника

Биссектриса треугольника обладает одним замечательным свойством: она делит противолежащую сторону на отрезки, пропорциональные соответствующим боковым сторонам (рис. 177).

с/а = d/b или c/d = a/b.

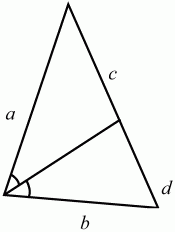
Рис. 177.

Это свойство часто используется в задачах, в которых фигурирует биссектриса треугольника.

Примеры решения задач

107. В треугольнике ABC проведена биссектриса AD. Найдите периметр треугольника ABC, если АС = 4; DC = 2; BD = 3 (рис. 178). (1)

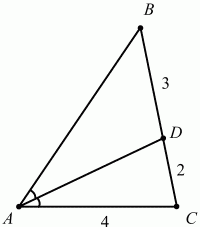
Рис. 178.

Решение. По свойству биссектрисы BD/AB = DC/AC; 3/AB = 2/4; АВ = 6.

Периметр треугольника РАВС = 6 + 5 + 4 = 15.

Ответ: 15.

108. Дан треугольник ABC, в котором ?В = 30°, АВ = 4, ВС = 6. Биссектриса угла В пересекает сторону АС в точке D. Определите площадь треугольника ABD (рис. 179). (2)

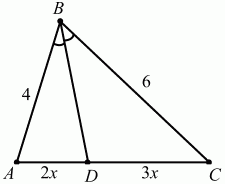
Рис. 179.

Решение. По свойству биссектрисы AD/DC = AB/BC = 4/6 = 2/3.

Пусть AD = 2х; DC = Зх.

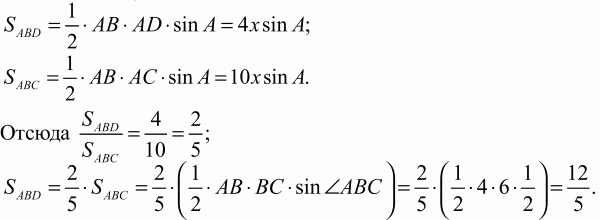
Ответ: 12/5.

Задачи для самостоятельного решения

109. В треугольнике ABC, где АВ = 6, АС = 4, биссектриса AL и медиана ВМ пересекаются в точке О. Найдите BO/OM (1).

110. Определите стороны треугольника, если медиана и высота, проведённые из вершины одного угла, делят этот угол на три равные части, а сама медиана равна 10 см. (2)