Ответы и указания к задачам экзаменационного комплекта № 2
Билет № 1
3) 37,9 дм.
4)
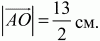
5) 12 см.
Билет № 2
3) 12 и 8 см.
4) а) 6 см; б) 8 см; нет.
5) К (18, 12).
Билет № 3
3)
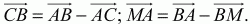
4) б) 80° и 100°.
5) Докажите равенство ?AFC и ?АМС.
Билет № 4
3) 41° и 49°.
4) а) угол D = 30°, угол CAD = 15°; б)
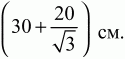
5) 210 см2.
Билет № 5
3) 4 и 3 см (воспользуйтесь свойством биссектрисы).
4) 6 см.
5) Уменьшится в 21 раз.
Билет № 6
3) Получится равная трапеция.
4) 25?2 см2.
5) Докажите равенство ?АОВ и ?EOD.
Билет № 7
3) 53° (ВС параллельна AD).
4) x = 2; y = -0,5;z = -1.
5)
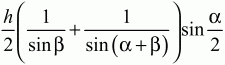
(пусть
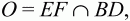
далее для нахождения ЕО и OF воспользуйтесь теоремой синусов).
Билет № 8
3)
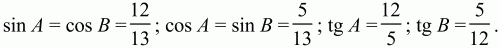
4) 60 см2.
5) 15° (?АВР – равнобедренный, а т. к. угол В равен 50°, то угол PAC = 65° – 50° = 15°).
Билет № 9
3) Да.
4) (9 + 3?3) см.
5) 60° (угол ВАО равен углу СВО и пусть он равен ?;
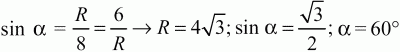
и угол ВОС равен 180° – 60° – 60° = 60°).
Билет № 10
з) ?3.
4) ?7 см.
5) 10/?7 = (по теореме косинусов третья сторона равна ?21, значит
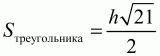
и т. д.).
Билет № 11
3) 32° (СО – часть высоты).
4) 15 и 24 м.
5) Докажите, что ?MDP = ?NBK, ?ANM = ?КСР и воспользуйтесь признаком параллелограмма).
Билет № 12
3) 73°.
4) 30?2 см2.
5)
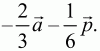
Билет № 13
3) 40?3 см2.
4) Нет, т. к. треугольника со сторонами 1, 4 и 5 не существует (сумма двух любых сторон треугольника всегда больше третьей стороны).
5) 5 см (достройте трапецию до правильного шестиугольника).
Билет № 14
3) Да (k = 2).
4) 4?3 + 6.
5) 62°, 49°, 69°.
Билет № 15
3) 43°.
4) DE = 96/5 м (проще всего заметить, что ?ADE ~ ?ABC).
5) 22 см.
Билет № 16
3) 12; 12?3; 24 см.
4) а) равенство следует из подобия треугольников ВНС и DCP.
б) 4/5.
5) Проведите из центра квадрата прямые, параллельные сторонам квадрата и найдите равные треугольники.
Билет № 17
3)
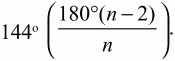
4) а) МТ и РК параллельны, a MP и КT – нет; б) да.
5) 110° и 70°.
Билет № 18
3) Угол DBC равен 17°, угол ABC равен 34°, АС = 18 см.
4) а) 0; б) – 2 (угол между векторами 120°).
5) 2, 3, 4, 5 или 6 см.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК