2.8. Задачи на пропорциональность отрезков хорд и секущих окружности

Напомним свойства хорд и секущих (рис. 196).

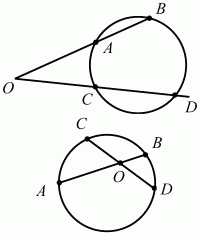
Рис. 196.

Для обоих случаев ОА ? ОВ = ОС ? OD.

В частности, если А совпадает с В (ОА – касательная), то ОА2= ОС ? OD.

Примеры решения задач

139. Дано (рис. 197):

ОА = 4, АВ = 3, CD = 2. Найдите ОС. (1)

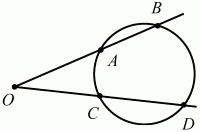
Рис. 197.

Решение. Пусть ОС = х, тогда ОА ? ОВ = ОС ? OD; 4 ? 7 = х(х + 2);

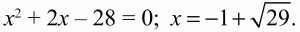
Ответ:

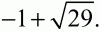
140. Стороны прямоугольника равны а и b. На стороне а, как на диаметре, построена окружность. На какие отрезки окружность делит диагональ прямоугольника (рис. 198)? (2)

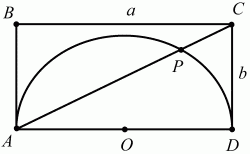
Рис. 198.

Решение. Из точки С проведена секущая СА и касательная CD к окружности. По известному свойству имеем: СР ? СА = CD 2;

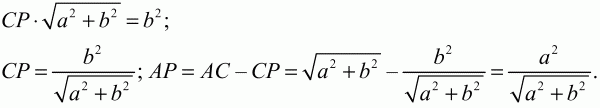
Ответ:

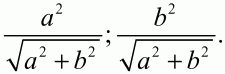
Задача для самостоятельного решения

141. ОА – касательная; ОВ = 4; ВС = 3. Найдите длину ОА (рис. 199). (1)

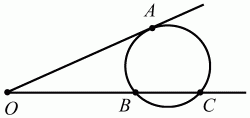
Рис. 199.