Задача 131 (рис. 290)

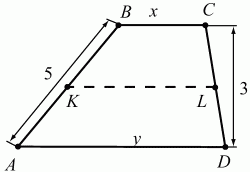
Рис. 290.

Решение. Пусть ABCD – данная трапеция, АВ = 5, CD = 3, KL – средняя линия. Обозначим величины отрезков ВС и AD через х и у соответственно. Так как в четырёхугольник ABCD можно вписать окружность, то х + у = ВС + AD = АВ + CD = 8. Поскольку KL – средняя линия трапеции, то KL = (BC + AD)/2 = 4. Если h – высота трапеции ABCD, то из теоремы о пропорциональных отрезках, отсекаемых параллельными прямыми, следует, что высоты трапеций KBCL и AKLD равны h/2. Для площадей этих трапеций имеем

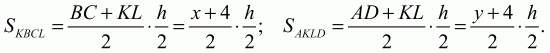
По условию

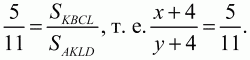
После упрощений получаем уравнение 11x – 5у = -24. Система уравнений

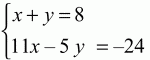
имеет единственное решение х = 1, y = 7.

Ответ: BC = 1, AD = 7.