Задача 35 (рис. 235)

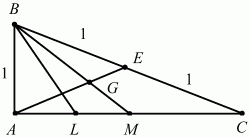
Рис. 235.

Решение. Пусть ABC – данный в условии задачи треугольник. По теореме Пифагора находим, что AC = ?3. Поскольку sin ?ABC = ?3/2, то, учитывая, что угол ?ABC – угол прямоугольного треугольника, находим, что ?ABC = ?/3. Следовательно, ?АСВ = ?/6. Так как BL – биссектриса угла ABC, то ?ABL = ?/6. Из прямоугольного треугольника ABL находим

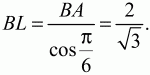
Пусть М – середина отрезка АС. Тогда AM = 1/2 АС = ?3/2. Из прямоугольного треугольника ВАМ находим, что

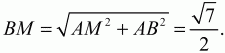
Так как точка пересечения медиан делит каждую из них в отношении 2:1, то

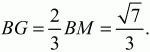
Для ответа на вопрос, поставленный в задаче, надо сравнить числа

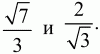
Поскольку

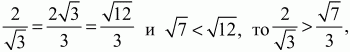
т. е. BL > BG.

Ответ: длина BL больше длины BG.