28. Решение задачи о жадном фальшивомонетчике

Каждая из проверяемых монет изымается из нового ящика и с вероятностью m/n фальшива. Так как монеты извлекаются независимым образом, то искомая вероятность отвечает биномиальному распределению.

Исследуем поведение этой вероятности при возрастании n и фиксированных r и m.

Для этого запишем ее в виде

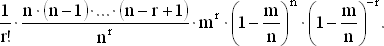
С ростом n 1/r! и m^r не меняются, а

n·(n ? 1)· ... ·(n ? r + 1)/n^r стремится к 1, как указано в задаче 27, 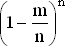стремится к e^?m и стремится к 1 (так как m и r фиксированы). Поэтому при больших n

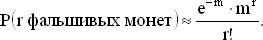
Сумма этих вероятностей равна:

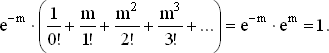
Ряд, записанный в скобках, является разложением e^m.

Распределение Пуассона

Распределение, задаваемое вероятностями

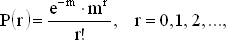
называется законом Пуассона и служит хорошей математической моделью для многих физических процессов.