32. Решение задачи «В поисках парных дней рождения»
Автор считает, что большинство людей имеет в виду именно эту задачу, когда им предлагают задачу 31 о парных днях рождения. Мысль о дне рождения, совпадающем с вашим, и вызывает удивление при ответе r = 23 в задаче о парных днях рождения. В настоящих условиях вам совсем не важно, совпадают ли дни рождения других людей, если только они не совпадают с вашим. Чаще всего считают, что ответ в этой задаче равен половине от 365 или 183. Из-за смешения двух проблем ответ r = 23 кажется тогда неправдоподобно маленьким.
Но и в настоящей задаче интуитивный ответ 183 оказывается неправильным. Дело в том, что выборка дней рождения производится с возвращением. Если первый из опрошенных родился 4-го июля, то ничто не мешает и последующим иметь тот же день рождения. Вероятность того, что опрошенный человек родился не в один день с вами, равна (N ? 1)/N, где N = 365 — число дней в году. При опросе n людей вероятность того, что все они произошли на свет не в ваш день рождения, равна [(N ? 1)/N]n, и вероятность того, что хотя бы у одного день рождения тот же самый, что и ваш, равна
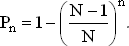(4)
Нас интересует наименьшее значение n, для которого Pn не меньше 1/2. Логарифм 364 равен 2.56110, а 1/2 равен ?0.30103.
Если мы перейдем к логарифмам, то обнаружим, что искомое значение n равно 253, что довольно значительно отличается от 183.
Можно поступить и иначе, использовав опять аппроксимацию
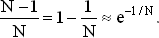
Тогда
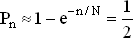
и
Логарифмируя, получаем n/N ? 0.693, n ? 0.693N. Для N = 365 получаем n = 253.
Эта задача легче предыдущей, и обсуждение связи между их ответами представляется поучительным.