23. Решение задачи о ничьих при бросании монеты

Ниже мы обобщим метод решения задачи 22 и покажем, что вероятность отсутствия ничейного результата (при N четном и N нечетном) равна

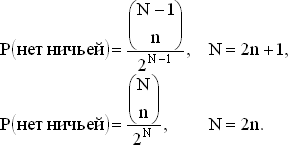
Эти формулы показывают, что указанная вероятность одна и та же для четного N и для следующего за ним нечетного числа N + 1. Например, когда N = 4, надо применить вторую формулу. Шестнадцатью возможными исходами являются

 ААAA      BAAA      ABBA      BABB

*AAAB      AABB      BABA     *BBAB

*AABA      ABAB      BBAA     *BBBA

 ABAA      BAAB      ABBB     *BBBB

где звездочкой отмечены комбинации с равновесным положением.

Поскольку число сочетаний из 4 по 2 равно 6, то вторая формула действительно верна для этого значения N.

При N = 2n вероятность x выигрышей A есть . Если x ? n, то вероятность ничьей есть 2x/N (на основании задачи 22), а при x ? n эта вероятность равна 2·(N ? x)/N. Чтобы получить вероятность ничьей, находим вероятность x выигрышей, умножим ее на условную вероятность ничьей при x выигрышах и просуммируем полученные выражения, что дает

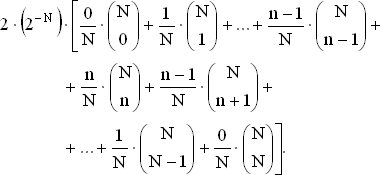          (1)

Если подставить в это выражение формулу для биномиальных коэффициентов и произвести необходимые сокращения, то с точностью до слагаемого

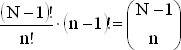
получим 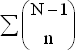, где суммирование ведется по всем возможным значениям x. Следовательно, мы можем переписать выражение (1) в виде

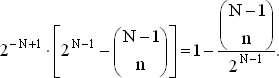          (2)

Отсюда видно, что вероятность отсутствия ничьей есть

 ,

что после небольших преобразований может быть записано в виде

,

как было указано выше.