33. Решение задачи о соотношении между разными задачами о парных днях рождения
По существу, вопрос состоит в определении числа возможных случаев в задаче о парных днях рождения. В задаче об индивидуальном дне рождения для n людей имеется n возможностей встретить человека, день рождения которого такой же, как у вас. В задаче о парных днях рождения каждый человек сравнивает свой день рождения с r ? 1 днями рождения остальных людей. Число пар равно, таким образом, r·(r ? 1)/2, что и является числом возможных случаев. Для того чтобы вероятности в двух задачах приблизительно равнялись, должно выполняться соотношение
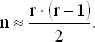 (1)
(1)
Например, при r = 23 число n должно равняться 23·22/2 = 253, что согласуется с полученным ранее.
Мы уже видели, что при n значительно меньшем по сравнению с N, вероятность того, что ни один из n людей не родился с вами в один и тот же день, приближенно равна e?n/N. С другой стороны, в задаче о парных днях рождения было показано, что для значений r, малых по сравнению с N, вероятность отсутствия парных дней рождения приблизительно равна e?r·(r ? 1)/2N. Для равенства этих двух вероятностей должно иметь место соотношение (1). Полученная аппроксимационная формула поясняет связь этих двух задач. Из сказанного ранее следует, что r·(r ? 1)/2 имеет смысл числа возможных случаев, что также дает основание для сопоставления n и r·(r ? 1)/2.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК