1. Решение задачи о ящике с носками

Рассмотрим сначала численный пример. Пусть в ящике 5 красных и 2 черных носка; вероятность того, что первый вынутый носок — красный, равна 5/(5 + 2). Если первый носок — красный, то условная вероятность того, что второй носок также красный, равна 4/(4 + 2), так как один красный носок уже вынут. Произведение этих двух чисел дает вероятность того, что оба носка красные:

Это число близко к ?, но в условии задачи фигурирует ровно ?. Подойдем теперь к задаче алгебраически.

Пусть в ящике r красных и b черных носков. Вероятность того, что первый носок — красный, равна r/(r + b) и при осуществлении этого события условная вероятность того, что второй вынутый носок также красный, есть (r ? 1)/(r + b ? 1). Согласно условиям задачи вероятность того, что оба носка — красные, равняется ?, или

Можно начать со значения b = 1 и искать нужное значение r, затем перейти к случаю b = 2 и рассмотреть различные значения r и т. д. Это довольно быстро приводит к решению. Но можно подойти к задаче и на более солидном математическом уровне.

Заметим, что

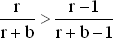  при b > 0.

Отсюда следует неравенство

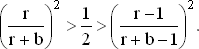
Извлекая квадратные корни, для r > 1 получаем

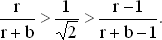
Из первого неравенства имеем

или

Из второго неравенства находим

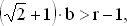
так что

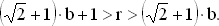
Для b = 1 получаем

2.414 < r < 3.414,

так что можно взять r = 3. При r = 3, b = 1 имеем

Таким образом, минимальное число носков есть 4.

Рассмотрим теперь четные значения b.

Таким образом, минимальное число носков в ящике есть 21 при условии, что b четно. Если интересоваться всеми значениями r и b такими, что вероятность извлечения двух красных носков равна ?, то следует использовать методы теории чисел. Этот вопрос приводит к знаменитому уравнению Пелла[4]. Возьмите, например, r = 85, b = 35.