49. Решение задачи об удвоении точности

Да. Пусть A — длина длинного стержня, а B — длина короткого. Можно положить эти стержни рядом и измерить разность длин A ? B, а затем приложить их один к другому и измерить сумму длин A + B. Пусть D и S обозначают наблюденные длины A ? B и A + B соответственно. Тогда оценка для A есть 1/2(S + D) и оценка для B есть 1/2(S ? D). Далее, D = A ? B + d, S = A + B + s, где d и s — случайные ошибки. Следовательно,

В среднем ошибка 1/2(d + s) будет нулевой, поскольку d и s имеют средние нуль. Дисперсия оценки A есть дисперсия

Это значение совпадает со значением для дисперсии среднего двух независимых наблюдении. Таким образом, оба наблюдения внесли полный вклад в измерение A. Точно так же дисперсия оценки B равняется ??/4. Следовательно, делая два измерения — одно для разности, другое для суммы — мы получаем оценки, точность которых равна точности при четырех рениях, по два на каждый стержень в отдельности.

Для получения столь хороших результатов мы должны как можно точнее соединить концы стержней. Если этого сделать нельзя, то можно считать, что в результаты измерений входит ошибка, связанная с неидеальным совпадением концов стержня. Если эта случайная ошибка имеет штандарт ??2, то одному измерению суммы или разности отвечает штандарт ??3/?2, и дисперсия нашей оценки A будет равна

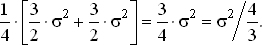
При этих предположениях наша точность будет точно такой же, как и точность при 4/3 независимых измерениях вместо 2, но все же больше точности одного прямого измерения.

Мы можем обосновать предположение о том, что ошибка от неточного совпадения концов имеет штандарт ?/?2, следующим образом. Представим себе s (или d) как сумму двух независимых ошибок измерения, каждую с дисперсией ??/2. Тогда сумма слагаемых ошибок имеет дисперсию, которую мы считали

равной ??. Если мы припишем дисперсию ??/2 и третьему слагаемому, то такая модель будет согласовываться с исходной.