9. «Крэпс»

Эта игра, как мы скоро увидим, удивительно близка к безобидной, хотя все же и невыгодна для игрока.

Подсчитаем сначала вероятности для полного числа очков на двух костях. Сделаем кости различимыми, окрасив их, скажем, в красный и зеленый цвета. Тогда подбрасывание 2-х костей имеет 6?6 = 36 равновероятных исходов, которые приведены ниже в таблице.

В клетках указана соответствующая сумма очков.

Простым подсчетом мы находим распределение вероятностей суммы очков при одновременном подбрасывании двух костей.

Здесь P обозначает вероятность появления соответствующей суммы очков.

Вероятность выигрыша после первого бросания равна

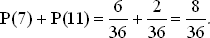
Вероятность проигрыша после первого бросания равна

Для дальнейших бросаний нам надо знать вероятность того, что выпадет «пойнт». Так как нам важны лишь очки, отвечающие «пойнт» или 7, то можно вычислять условные вероятности выбросить «пойнт» при условии, что при первом бросании появился «пойнт». Иногда этот метод называется методом «приведенного выборочного пространства», так как хотя в принципе возможны все варианты от 2 до 12 очков, мы рассматриваем лишь «пойнт» и 7.

Например, если выпало 4 очка, то существует 3 возможных способа их появления и 6 способов для появления 7 очков. Таким образом, условная вероятность выбросить «пойнт» равна 3/(3 + 6) = 3/9.

Аналогично условные вероятности других очков «пойнт» равны

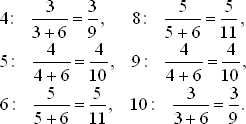
Для определения безусловной вероятности выигрыша при данной сумме «пойнт» надо умножить вероятность получения «пойнт» при первом бросании на условную вероятность выигрыша. Суммируя эти величины, находим вероятность выигрыша для суммы «пойнт»:

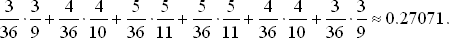
Прибавляя к этому значению вероятность выигрыша при первом бросании 8/36 ? 0.22222, видим, что полная вероятность выигрыша игрока равна 0.49293. Его средний ущерб равен 0.50707 ? 0.49293 = 0.01414 или 1.41 %. Автор считает, что это наиболее справедливая игра без стратегии, которая практикуется в игорных домах.

Некоторым читателем может показаться слишком искусственным подход, связанный с условными вероятностями. Мы дадим и другой метод, связанный с суммированием бесконечных рядов.

Пусть P обозначает вероятность получить «пойнт», а R — вероятность появления суммы очков, при которой игра продолжается (R = 1 ? P ? 1/6). Здесь 1/6, конечно, имеет смысл вероятности появления 7. Игрок выигрывает при r + 1 бросании, если игра продолжалась r шагов, и при r + 1 шаге появился «пойнт». Вероятность этого события равна R^rP, r = 0, 1, 2, ... Суммируя по r, получаем

P + RP + R?P + ... = P(1 + R + R? + ...)

или

вероятность получить «пойнт» = P/(1 ? R).

Например, если «пойнт» равен 4,

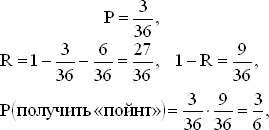
что согласуется с полученным ранее.

Сам автор решал сначала эту задачу с помощью суммирования бесконечного ряда и был обрадован, когда несколько дней спустя обнаружил указанный здесь более простой подход.