45. Решение задачи о среднем числе совпадений
Рассмотрим сначала задачу с колодой карт. Если в колоде 52 карты, то каждая карта с вероятностью 1/52 занимает место, уже занятое такой же картой. Так как общее число возможных мест для каждой карты равно 52, то среднее число совпадений равно 52·1/52 = 1. Таким образом, в среднем происходит только одно совпадение. Если бы колода состояла из n различных карт, то среднее число совпадений прежнему равнялось бы 1, так как n·(1/n) = 1. Этот вывод основывается на теореме о том, что среднее суммы есть сумма средних.
Более формально, с каждой парой карт может быть связана случайная величина Xi, которая равна 1 в случае, если карты одинаковы, и 0, если карты различны. Имеем

Наконец, общее число совпадений равно ?Xi и в силу уже упоминавшейся теоремы
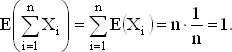
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК