29. Решение задачи о заплесневевшем желатине

Разобьем поверхность пластинки на n малых равных площадок. Для каждой площадки вероятность колонии равна p, а их среднее число есть np = 3. Нас интересуют лишь маленькие площадки. Когда n растет, p становится малым, так как площадь участков стремится к нулю. Вместо того, чтобы считать среднее число колоний равным 3, будем рассматривать общее среднее m = np. Может показаться, что на некоторых площадках встречаются две или больше колоний, но эти сомнения можно оставить, потому что площадки столь малы, что едва умещают одну колонию. Тогда вероятность ровно r колоний на n маленьких площадках равна

где p = m/n. Заменим p на m/n в этой формуле. Полученное выражение уже знакомо нам по задаче 28. Пусть n ? ?. Тогда мы снова приходим к распределению Пуассона

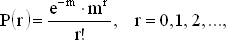
При m = 3 и r = 3 получаем значение 0.224.

То, что m действительно является средним этого распределения, проверяется непосредственно:

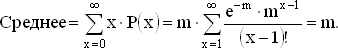
Чтобы получить численные результаты для больших значений m, где r = m, можно использовать таблицы[10] или формулу Стирлинга. Последняя дает

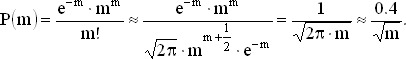
Численные примеры: