41. Обсуждение задачи о поездах

Хотя на поставленные вопросы вряд ли можно дать «правильный» ответ, все же возможно разумное объяснение этих задач. Например, согласно принципу симметрии, если на отрезок бросается одна точка, то в среднем два полученных отрезка имеют одинаковую длину, так что в пункте (а) ответ равен 119, так как длина левого промежутка равна 59, 2·59 = 118 и 118 + 1 = 119.

Аналогично в пункте (б) можно предположить, что пять наблюденных номеров разбивают весь отрезок на шесть равных частей. Так как 60 ? 5 = 55, то средняя длина первых пяти отрезков равна 11, и общее число номеров может быть оценено как 60 + 11 = 71 (рис. 16). Конечно, оценка не может быть абсолютно точной при многократном употреблении.

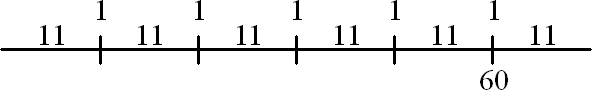
Рис. 16.

Указанный метод заставляет думать, однако, что в среднем при многократном использовании такие оценки мало отличаются от истинного значения N при большом числе наблюдений. Если неизвестное число N подлежит оценке во многих задачах, то, следуя каждый раз приведенному методу (извлечь выборку, построить оценку), мы в среднем будем близки к истинному значению при достаточно больших объемах выборок.

С другой стороны, может быть и так, что вас не интересует приближение в среднем или недоступно большое число наблюдений, но вы хотите угадать значение N, несмотря на то, что это маловероятно. Тогда разумно оценить N как наблюденный максимум из номеров. Если вы, например, знаете номера двух локомотивов, то вероятность того, что один из двух номеров — максимально возможный, равна 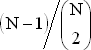или 2/N.

Иногда пользуются методом доверительного оценивания, при котором в качестве оценки предлагается некоторый интервал для неизвестного параметра. Ограничимся случаем одного наблюдения. Если наудачу извлечь один из номеров 1, 2, ..., N, то вероятность появления каждого номера равна 1/N. Поэтому вероятность того, что наш номер принадлежит некоторому множеству, равна числу элементов этого множества, деленному на N. Так, если, скажем, n — это случайный номер, а N — четное число, то P(n > N/2) = 1/2, для нечетных значений N эта вероятность несколько больше. Таким образом, если n случайно, то вероятность события n > N/2 не меньше 1/2. Если мы наблюдаем значение n, а N не известно, то в качестве верхней границы для N мы можем предложить 2n. В каждом отдельном случае утверждение 2n > N верно или нет, однако, оно справедливо более, чем в половине случаев. Если желать увеличения процента правильных высказываний, то надо изменить доверительный предел.

Так, например,

и утверждение 3n ? N справедливо по крайней мере в 2/3 случаях. В нашей задаче, если мы хотим быть уверенными в справедливости нашего высказывания о значении числа N в 2/3 из 100% случаев, то можем сказать, что N лежит в промежутке с концами 60 и 180.

Другим часто используемым методом для оценивания является метод максимального правдоподобия, согласно которому значение N выбирается таким образом, чтобы сделать наблюденную выборку наиболее вероятной. Так, например, если N = 100, то наше наблюденное значение 60 имеет вероятность 1/100, в случае же N = 60 эта вероятность равна 1/60. Мы не можем оценить N значением, меньшим 60, так как для N = 59 или меньшем вероятность появления номера 60 равна нулю. Следовательно, если n — наблюденный номер, то оценкой максимального правдоподобия для N является само n.

В задаче не предполагалось наличие добавочной информации, такой, как «это большая железная дорога, и на ней по крайней мере 100 поездов, но, наверное, меньшее, чем 100 000», которая, конечно, может быть полезна.