К главе 17

17.1. Осуществить замену переменных: x ? 1 = y, 2x + 1 = z. Найти f(y) и g(z), что равносильно знанию f(x) и g(x).

17.2. Уравнение f(f(x)) = 0 имеет корни x₁ = 0 и x₂ = 3. Исследование функции y = x? ? 6x? + 9x ? 3 позволит определить число оставшихся корней интересующего нас уравнения.

17.3. Первое уравнение после подстановки примет вид

5 · 2^{x? ? 2xy + 1} = (1 + 2k)3^{y? ? 1},

k — целое. При каких y в правой части не будет множителя 3?

17.4. Полученное после подстановки квадратное уравнение относительно z имеет дискриминант, равный (3y ? ¹/_y)? , что позволяет непосредственно рассмотреть возможные корни.

17.5. Касание функций f(x) и F(x) в точке М₀(x₀; y₀) означает совпадение ординат f(x₀) и F(x₀), а также угловых коэффициентов касательных при x = x₀, т. е. значений f?(x₀) и f(x₀).

17.6. Будьте внимательны в отношении точек границы множества решений и определите, какие из них принадлежат этому множеству, а какие не принадлежат.

17.7. Прямая y = ?x позволит отсечь от части плоскости, координаты точек которой удовлетворяют первому неравенству — фигуру, площадь которой нас интересует.

17.8. Прямые AC и BD пересекаются в точке E(4; 4). Прямая BC параллельна оси абсцисс и пересекает ось ординат в точке G. Через точку D проведем прямую DF, параллельную оси абсцисс и пересекающую ось ординат в точке F, а прямую AC — в точке H. Пусть CK — перпендикуляр, опущенный из точки С на FD. Теперь искомую площадь легко найти через площадь прямоугольника FGCK и прямоугольных треугольников, которые будут изображены на рисунке после всех проведенных выше построений.

17.9. После замены переменных и простых преобразований исходные неравенства примут вид

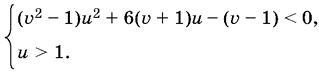
Проекция множества решений этой системы рассматривается на прямую u = 2. Левую часть первого из неравенств рассмотрите как функцию второго порядка относительно u, где зависящие от v коэффициенты — параметры. Тогда можно сформулировать условия существования решений в зависимости от значений v. (Куда направлены ветви параболы и каков знак дискриминанта.) (!!)

Придется рассмотреть существование решений первого неравенства при u > 1 для разных случаев относительно коэффициента при u? функции f(u), т. е. v? ? 1 > 0; v? ? 1 = 0; v? ? 1 < 0.

17.10. Если а — целое, то дискриминант данного уравнения есть квадрат целого числа, т. е. а? ? 2а ? 19 = n?. Отсюда (а ? 1)? ? n? = 20. Левую часть нужно представить в виде произведения целых чисел.

17.11. Случаи, когда y = 0 нужно рассмотреть отдельно. Определить соответствующие а и для каждого из них решить исходное уравнение. До этого выводов о числе корней исходного уравнения делать не следует.

17.12. Исходное уравнение при y = sin 4x преобразуется к виду

(а + 3)y? + (2а ? 1)y + (а ? 2) = 0,

где |y| ? 1.

Исследуйте отдельно случаи D = 0 и D > 0, для каждого из которых найдите значения а, удовлетворяющие условию, в силу которого равно восемь решений исходного уравнения (см. условие задачи) попадают на отрезок [??, ?]. (!!)

При замене переменной z = 4x получаем уравнение

(а + 3) sin? z + (2а ? 1) sin z + (а ? 2) = 0,

или

(а + 3)y² + (2а ? 1)y + (а ? 2) = 0,

где y = sin z; |y| ? 1.

Если существует решение второго уравнения y₁ ? (?1, 1), т. е. y₁ лежит внутри интервала (?1, 1), то этому y₁ соответствуют ровно два значения z ? (??, ?) и ровно восемь значений x ? (??, ?). (Для z период синуса равен 2?, а для x = ^z/₄ период синуса уменьшится в 4 раза и будет равен ^?/₂, т. е. внутри каждого интервала длиной ^?/₂ мы получим два решения для x, а внутри интервала (??, ?) таких решений будет восемь.)

17.13. Если (x, y) — фиксированная точка плоскости и через эту точку проходит кривая семейства, то должно существовать, по крайней мере одно соответствующее ей значение параметра а. Рассмотрев уравнение семейства кривых как уравнение относительно а, мы и получим соответствующие ограничения.