К главе 19

19.1. Свести задачу к сравнению (^{n + 1}/_n)ⁿ и числа 2.

19.2. Нужно использовать условие, в силу которого а_р, a_q, а_r и a_s образуют геометрическую прогрессию. Это удобнее сделать так: a?q = а_ра_r и т. п. (!!)

Остается выразить p ? q, q ? r и r ? s через а_р, a_q, а_r и a_s и убедиться, что (p ? q)(r ? s) = (q ? r)?.

19.3. При составлении разностей а ? b, b ? с и с ? а удобнее пользоваться представлением чисел a, b и с с помощью арифметической прогрессии.

19.4. Воспользоваться тем, что log_x ^b/_a = log_x ^с/_b (числа a, b, с образуют геометрическую прогрессию).

19.5. Вынести за скобки ⁷/₉.

19.6. Под знаком квадратного корня стоит полный квадрат ¹/₉(10²ⁿ ? 2 · 10ⁿ + 1).

19.7. После исключения получим уравнение относительно а1 и а₃, из которого следует, что а₁ = а₃.

Так как а₁ = а₃, то 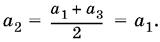 Рассмотрите систему: а₁ = а₂, а₂ = а₃.

19.9. Теорема Виета, записанная для данного уравнения, приведет к системе уравнений относительно x₁ и q (уравнение, в которое входит а, можно не рассматривать). Удобнее найти сначала q.

19.10. Записать произведение n первых членов и воспользоваться тем, что а₁ = ?2.

19.11. Если цифру сотен обозначить через а, а разность прогрессии — через d, то число делится на 5, когда либо а + 2d = 0, либо а + 2d = 5; оно же делится на 9, если а + (а + d) + (а + 2d) делится на 9. Остается воспользоваться тем, что а, а + d и а + 2d — цифры.

19.13. B задаче спрашивается, сколько комбайнов было в колхозе. Эту величину мы обозначим через n. Условия задачи позволяют составить три уравнения. При этом левая часть уравнения, соответствующего работе по плану, представляет собой сумму членов арифметической прогрессии. (!!)

При решении системы уравнений нужно исключить x и y.

19.14. При решении уравнений нужно иметь в виду, что нас интересуют только а и q.

19.15. Двух уравнений достаточно для решения задачи, так как нас интересуют не сами числа а, b и с, а отношение каких-либо двух из них. Поскольку полученные результаты использования условий задачи уравнения однородны относительно а, b и с, то определить интересующую нас величину нетрудно.

19.16. Так как предел (?)ⁿ при n ? ? равен нулю, то а_n и b_n имеют общий предел.

19.17. Члены двух арифметических прогрессий, имеющих первый член, равный нулю, могут снова образовать арифметическую прогрессию в том и только в том случае, если разность одной прогрессии кратна разности другой прогрессии.