Глава 8 Делимость многочленов. Теорема Безу. Целые уравнения
8.1. Положив x ? 5 = y, приведем уравнение к виду
(y + ?)4 + (y ? ?)4 = 1, или (2у + 1)4 + (2у ? 1)4 = 16,
откуда после простых преобразований получим
16y4 + 24y2 ? 7 = 0.
Ответ. x1,2 = 5 ± i?7/2; x3 = 4,5; x4 = 5,5.
8.2. Перемножим попарно первую и третью скобки и две оставшиеся:
(12х? + 11х + 2)(12х? + 11х ? 1) = 4.
Обозначив 12х? + 11х + ? = y, получим
(y + 3/2)(y ? 3/2) = 4,
откуда
y1 = ?5/2, у2 = 5/2.
Остается решить два квадратных уравнения.
Ответ. 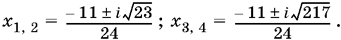
8.3. Запишем уравнение в виде
x? ? 17 = 3y?
и рассмотрим случаи x = 3k, x = 3k ± 1. B первом случае левая часть примет вид 9k? ? 17 и не будет делиться на три. B остальных двух случаях в левой части получим
9k? ± 6k ? 16,
что снова не делится на три. Поскольку правая часть всегда делится на три, то уравнение не имеет целых решений.
8.4. Решим уравнение относительно x:
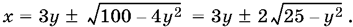
Так как уравнение имеет действительные корни лишь при
25 ? y? ? 0, т. е. |y| ? 5,
то остается перебрать все целые значения y, для которых 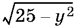 — целое число: y = 0, y = ±3, y = ±4, y = ±5. Для каждого значения y найдем два значения x.
— целое число: y = 0, y = ±3, y = ±4, y = ±5. Для каждого значения y найдем два значения x.
Ответ. (10, 0), (?10, 0); (?1, ?3), (?17, ?3); (1, 3), (17, 3); (?6, ?4), (?18, ?4); (6, 4), (18, 4); (?15, ?5), (15, 5).
8.5. По определению деления имеем тождество
x99 + x? + 10х + 5 = Q(x) (x? + 1) + ax + b,
которое справедливо всюду в области комплексных чисел. Так как частное Q(x) нам неизвестно и оно нас не интересует, то в качестве значения x нужно выбрать один из корней выражения x? + 1, например x = i. Подставив x = i, получим
i99 + i? + 10i + 5 = аi + b, т. е. 8i + 5 = аi + b,
откуда а = 8, b = 5.
Ответ. 8х + 5.
8.6. Перепишем уравнение в виде
y? 2x? + 1/x? + 2 = 6.
Если x? ? 1, то 2x? + 1/x? + 2 ? 1.
Так как x = 0 не является целочисленным решением уравнения, то можно утверждать, что y? ? 6. Остается рассмотреть случаи: y? = 0, y? = 1, y? = 4. Первый и второй не приводят к действительным значениям x. Для y? = 4 находим x? = 4.
Ответ. (2, 2), (2, ?2); (?2, 2), (?2, ?2).
8.7. Подставим в данное уравнение x = ?3 + 1. После простых вычислений и преобразований получим
36 + 10а + 4b + (22 + 6а + 2b)?3 = 0.
Сумма двух чисел, из которых одно рациональное, а другое иррациональное, может равняться нулю, только если оба числа равны нулю:
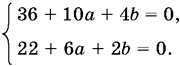
(1).
Решая эту систему, найдем а = ?4, b = 1. Поскольку уравнение
x4 ? 4x? + x? + 6x + 2 = 0
одним из своих корней имеет число ?3 + 1, а все коэффициенты уравнения — целые, то следует ожидать, что наряду с этим корнем должен существовать и корень ?3 ? 1. Подставим это значение x в уравнение и соберем отдельно рациональные и иррациональные члены. Получим
36 + 10а + 4b ? (22 + 6а + 2b)?3 = 0,
что приводит к той же системе уравнений (1) и имеет место при а = ?4, b = 1. Следовательно, x = 1 ? ?3 — второй корень данного в условии уравнения.
Разделив многочлен x4 ? 4x? + x? + 6x + 2 на
(x ? ?3 ? 1)(x + ?3 ? 1) = x? ? 2x ? 2,
получим квадратный трехчлен x? ? 2x ? 1, корнями которого являются числа 1 + ?2.
Ответ. x1,2 = 1 ± ?3; x3,4 = 1 ± ?2.
8.8. Из теоремы Виета получаем неравенства:
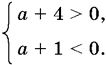
Добавляем к ним условие неотрицательности дискриминанта:
(а + 1)? ? 4(а + 4) ? 0.
Приходим к системе неравенств
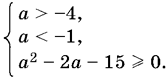
Последнему неравенству удовлетворяют числа а, лежащие вне промежутка между корнями: а ? ?3, а ? 5.
Ответ. ?4 < а ? ?3.
8.9. Пусть х1, х1q и х1q? — корни данного уравнения. По теореме Виета имеем систему
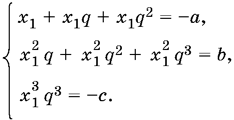
Из этих уравнений нужно исключить x1 и q. Поскольку из первого уравнения следует х1(1 + q + q?) = ?а, то второе примет вид
b = х1?q(1 + q + q?) = x1q(?а),
т. е. x1q = ? b/a, откуда
?b?/a? = ?c.
Ответ. са?= b?.
8.10. По теореме Виета
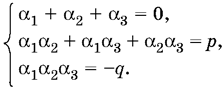
Возведем первое уравнение в квадрат:
?1? + ?2? + ?3? + 2(?1?2 + ?1?3 + ?2?3) = 0,
откуда найдем ?1? + ?2? + ?3? . Как видим, последнее уравнение не понадобилось.
Ответ. ?1? + ?2? + ?3? = ?2p.
8.11. Разделив x? + ax + 1 на x ? ?, получим в частном x? + ?x + а + ??, а в остатке ?? + a? + 1. Условия задачи будут выполняться тогда и только тогда, если
?? + a? + 1 = 0,
x? + ?x + а + ?? > 0 при всех x.
Чтобы выполнялось второе условие, дискриминант ?3?? ? 4а должен быть отрицательным, т. е. 3?? + 4а > 0.
Число а не может быть равно нулю, так как уравнение а? + а? + 1 = 0 не удовлетворяется при а = 0. Из первого уравнения a = ?1 + ??/?. Поэтому должно быть
3?? ? 41 + ??/? > 0.
Если ? > 0, то последнее неравенство эквивалентно такому:
3?? ? 4(?? + 1) > 0,
или ??? > 4, y которого нет решений.
Если ? < 0, то получим
3?? ? 4(?? + 1) < 0,
или 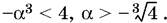
Ответ. 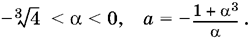
8.12. Пусть
P(x) = (x ? 2)(x ? 3) Q(x) + ax + b,
где ax + b — остаток, который надо найти.
По теореме Безу P(2) = 5, а P(3) = 7. Подставим x = 2 и x = 3 в правую часть написанного выше тождества. Получим систему относительно а и b
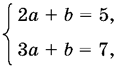
откуда а = 2, b = 1.
Ответ. 2x + 1.
8.13. Многочлен x4 + 1 делится на x? + рх + q тогда и только тогда, когда
x4 + 1 = (x? + ax + b)(x? + рх + q).
Раскрывая в правой части скобки и приравнивая коэффициенты при одинаковых степенях x, получим систему уравнений
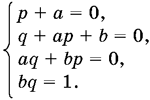
Из первого и последнего уравнений находим а = ?p, b = 1/q. Подставляя в оставшиеся два уравнения, получим
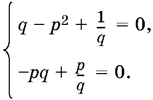
Второе уравнение можно переписать так: p(q ? 1/q) = 0.
Если p = 0, то первое уравнение не имеет действительных решений. Остается q = 1/q, т. е. q = ±1. Подставляя найденные значения q в первое уравнение, увидим, что, когда q = 1, р? = 2 и p = ±?2, а когда q = ?1, р? = ?2 и действительных решений нет. Итак, получаем две возможности: либо p = ?2 и q = 1, либо p = ??2 и q = 1.
Чтобы закончить решение, нужно сделать проверку. Можно было бы разделить x4 + 1 поочередно на каждый из двух трехчленов: x? + ?2 x + 1 и x? ? ?2 x + 1. Однако проще убедиться, что
x4 + 1 = (x? + ?2 x + 1)(x? ? ?2 x + 1).
Ответ. р1 = ? ?2, q1 = 1; р2 = ?2, q2 = 1.
8.14. После замены x ? 1 = y получим многочлен
(y + 1)2n + 1 ? (2п + 1)(y + 1)n + 1 + (2п + 1)(y + 1)n ? 1,
который должен делиться на y?. Вычислим его коэффициенты при y0, y1 и y2.
Свободный член этого многочлена равен
1 ? (2n + 1) + (2n + 1) ? 1 = 0;
коэффициент при y
2n + 1 ? (2n + 1)(n + 1) + (2n + 1)n = 0;
коэффициент при y?
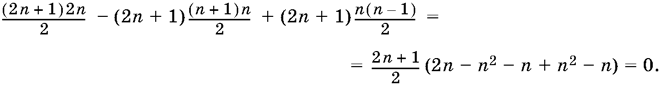
Тем самым утверждение доказано.
8.15. Чтобы данный многочлен делился на x? ? x + q без остатка, должно выполняться тождество
6х4 ? 7x? + рх? + 3x + 2 = (x? ? x + q)(6х? + ax + b).
B правой части стоит многочлен
6x4 + (а ? 6)x? + (b ? а + 6q)x? + (?b + qа)x + qb.
Так как многочлены равны тождественно, получаем систему
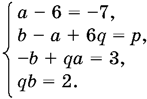
Из первого уравнения а = ?1. Из третьего и четвертого уравнений исключаем b. Приходим к уравнению
q? + 3q + 2 = 0,
откуда
q1 = ?1, q2 = ?2.
Сложив второе и третье уравнения, также исключим b:
5q ? 2 = p.
Следовательно,
р1 = ?7, p2 = ?12.
Итак, возможны два решения.
Ответ. 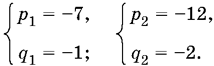
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК