К главе 24

24.1. Получившийся квадратный трехчлен можно разложить на множители. Однако такой прием исследования здесь не подойдет, так как аргумент, от которого зависит квадратный трехчлен, сам является функцией от x. Используйте другой прием для исследования квадратного трехчлена.

Выделите полный квадрат.

24.2. Данную функцию удобно записать в виде разности косинусов, поскольку в аргумент каждого синуса входит 2 x — единственное слагаемое, зависящее от x.

24.3. Для этого вынести sin x cos x за скобки.

24.4. А = x + y + 1.

24.5. Найдя наименьшее значение y в каждом из пяти интервалов, мы сравним эти значения друг с другом.

24.6. Для функции y = x + ^а/_x мы можем неравенство применить непосредственно и написать

x + ^a/_x ? 2?a .

Для данной же функции нужно иметь семь слагаемых, содержащих в знаменателе x, чтобы погасить влияние x⁷. (!!)

Представить ^a/_x в виде суммы семи одинаковых слагаемых ^a/_7x.

24.8. Выразить боковую поверхность как функцию только а + b.

24.9. Удобно ввести угол ? между диагональю шестиугольника и диагональю квадрата. Этот угол можно будет найти из условия, что диагонали квадрата взаимно перпендикулярны и должны принимать наибольшую возможную величину.

24.10. B условии сказано, что x — действительное число. Следовательно, дискриминант полученного квадратного уравнения не должен быть отрицательным. Это накладывает ограничения на y.

24.11. Чтобы решить систему

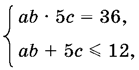
удобнее всего найти решение системы уравнений xy = 36 и x + y = 12, где x = ab, y = 5с.

24.12. Данная функция может быть записана в виде

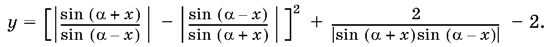
Обратите внимание на второе слагаемое. Когда оно достигает своего минимума?

24.13. Если acrsin x = ?, acrcos x = ?, то

?? + ?? = (? + ?)³ ? 3??(? + ?) = ^??/₈ ? ^3?/₂ ??.

Минимум функции достигается при ? > 0 (? не может быть отрицательным), а максимум — при ? < 0. Если ? > 0, то появляется возможность применить оценку, в силу которой ?? ? (^{? + ?}/₂)?.

24.15. После того как система приведена к виду

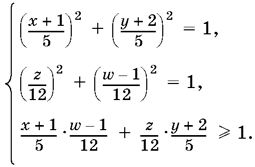
Теперь нужно ввести новые переменные. А лучше сразу обратить внимание на то, что эти переменные — синусы и косинусы двух углов. (!!)

Левая часть входящего в систему неравенства не что иное, как выражение для синуса суммы. Поэтому она не больше 1, т. е. последнее условие есть равенство. Не забудьте, что нужно найти min (y + w). Поэтому искать следует в области, где y < 0 и w < 0.