К главе 14

14.4. Когда мы заменим sin 2x и cos 2x на их выражения через tg x, могут быть потеряны те решения неравенства, при которых sin 2x и cos 2x существуют, а tg x не существует. Однако tg x входит в правую часть данного неравенства, а потому значения x, при которых tg x не существует, не могут быть решениями этого неравенства.

14.5. Способ 1. Чтобы найти секторы круга, в которых tg 2 x ? 0, нужно вначале построить радиусы, соответствующие углам, для которых tg 2x = 0 и tg 2x не существует.

Способ 2. B результате применения формулы тангенса двойного угла возможна потеря решений: из области определения выпадают точки, в которых cos x = 0.

14.8. Так как коэффициент при старшем члене положителен, то знаки корней зависят от знака свободного члена.

14.10. Найти те значения k, при которых полученное неравенство осуществимо.

14.11. Воспользоваться тем, что sin x + cos x = ?2 cos (x ? ^?/₄), и решить неравенство относительно y = cos (x ? ^?/₄).

14.12. Произведение cos x cos 3x, стоящее в знаменателе, выразить через cos 2x. Получится алгебраическое неравенство относительно y = cos 2x.

14.13. При возведении неравенства в квадрат достаточно потребовать, чтобы cos x ? 0.

14.15. Обозначить sin ? через y и разложить получившийся многочлен третьей степени на множители, воспользовавшись теоремой о делителях свободного члена и первого коэффициента.

14.16. Выражение 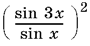 можно преобразовать, воспользовавшись разложением sin 3x = sin (2x + x).

14.17. Так как абсцисса вершины параболы оказывается внутри интервала ?1 < z < 1, а сама парабола направлена рогами вверх, то условие задачи равносильно тому, что ордината вершины положительна.