K главе 9

9.1. Точки ?2, ?1, 0 делят числовую ось на четыре интервала, в каждом из которых нужно решить данное уравнение. (!)

9.2. Если рассматривать значения x, обращающие в нуль числа, стоящие под знаками абсолютных величин, то придется разбить числовую ось на пять частей.

Удобнее ввести новое неизвестное у = x?. (!)

9.3. Это уравнение четвертой степени. Следовательно, нужно найти искусственный прием, приводящий к его решению. Удобно воспользоваться тем, что слева стоит сумма квадратов.

9.4. Возвести в куб и сравнить полученное уравнение с данным.

9.5. Свести уравнение к симметрической системе, обозначив первое слагаемое левой части через u, а второе через v. (!)

9.6. Если под радикалами раскрыть скобки, то получим квадратные трехчлены, отличающиеся лишь свободным членом. Поэтому данное в условии уравнение удобно заменить системой, обозначив первое слагаемое его левой части через u, а второе через v.

9.7. Поскольку неизвестное входит в уравнение либо в сочетании x ? b, либо в сочетании а ? x, то удобно ввести обозначения 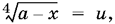 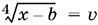 и получить систему алгебраических уравнений.

9.8. Ввести вспомогательное неизвестное у и свести решение данного уравнения к решению системы уравнений относительно x и у.

9.9. Перенести 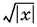 в правую часть уравнения и возвести обе части в квадрат.

9.10. Чтобы избавиться от знаков абсолютной величины, можно поступить двояко: либо потребовать, чтобы правая часть уравнения была неотрицательной, и решить уравнения

x? ? ^3x/₂ ? 1 = ?x? ? 4x + ?,    x? ? ^3x/₂ ? 1 = x? + 4x ? ?;

либо рассмотреть два случая: в первом выражение, стоящее под знаком абсолютной величины, неотрицательно, а во втором — отрицательно.

9.11. Рассмотреть различные случаи расположения x и у по отношению к нулю (всего придется рассмотреть четыре случая). (!)

9.12. Решить систему уравнений с параметром k, а затем решить систему неравенств. (!)

9.13. Рассмотреть различные случаи взаимного расположения чисел x и у и чисел x и ?у. Это позволит раскрыть знаки абсолютной величины. (!)

9.14. Второе уравнение — уравнение окружности радиуса ?а . Нарисовать кривую, которая определяется первым уравнением.

9.15. Одно решение очевидно: x = у = 0. Если ху ? 0, то можно разделить первое уравнение на ху, а второе на x?у?.

9.16. Если бы во втором и третьем уравнениях не было коэффициентов 2 и 3, то уравнения системы получались бы друг из друга с помощью циклической перестановки неизвестных x, у и z. Однако влияние коэффициентов оказывается столь сильным, что попытка использовать это свойство системы не приводит к успеху. Попытайтесь преобразовать систему в распадающуюся, для чего потребуется отыскать алгебраическое выражение, общее для двух уравнений, и исключить его.

9.17. Если первое уравнение системы записать в виде x + у = ?z и возвести в квадрат, то с помощью второго ее уравнения можно найти ху.

9.18. Сопоставьте первое и последнее уравнения. Если записать их в виде

x + у = 1 ? z,    х? + у? = 1 ? z?,

то напрашивается способ, с помощью которого можно преобразовать систему в распадающуюся.

9.19. Если раскрыть скобки, то получим систему линейных уравнений относительно u = x + у + z, v = ху + xz + yz, w = xyz. Найдя u, v и w, можно вычислить х? + у? + z?, если возвести x + у + z = u в куб: u? = х? + у? + z? + 3uv ? 3w.

Однако такой путь решения, хотя и прост по идее, требует значительных выкладок. Решение можно упростить, если ввести в рассмотрение многочлен M(t) = (t ? x)(t ? у)(t ? z) + а, который в силу условия задачи имеет корни t = а, t = b, t = с.

9.20. Первые два уравнения системы симметричны относительно x и у. Нужно использовать эту симметрию для того, чтобы получить одинаковые правые части у этих двух уравнений.

9.21. Если второе уравнение возвести в квадрат, то можно сравнить два выражения для (x + у)?. (!)

9.22. В первое уравнение входит у, в последующие уt, yt? и yt? соответственно. Эта закономерность позволяет исключить у.

9.23. Каждый элемент, стоящий в левой части второго уравнения, получается из соответствующего элемента, стоящего в левой части первого уравнения, возведением в квадрат. Нужно использовать это свойство системы.

9.24. Левые части всех трех уравнений симметричны относительно x, у, z. Поэтому, подвергнув какому-то преобразованию любые два уравнения системы, разумно сделать то же самое и с оставшимися двумя парами уравнений.

9.25. Если известна сумма s = x₁ + x₂ + ... + x_n, то из каждого уравнения можно найти соответствующее x_k.

9.26. Чтобы избежать возведения двучлена в третью и, тем более, в пятую степень, нужно ввести новые неизвестные так, чтобы выражение 7x ? 11у было одним из этих неизвестных.

9.27. Поскольку  входит в оба уравнения с разными знаками, а ?у — с одинаковыми, то естественно сложить данные уравнения и вычесть. При этом мы приходим к системе, у которой слева стоят сумма и разность одинаковых радикалов, а справа — разные радикалы.

9.28. Чтобы левые части уравнений стали однородными относительно неизвестных, удобно ввести новое неизвестное z = ?у.

9.29. Если каждое из уравнений возвести в квадрат, то получим систему относительно u = x? и v = у?. Проверка здесь может оказаться довольно сложной, поэтому целесообразно следить за равносильностью в процессе решения. Чтобы в результате возведения в квадрат не появились посторонние решения, достаточно записать ограничения: x > 0, у > 0.

9.30. Все члены системы, содержащие x и у, однородны второй степени относительно x и у. Пусть данная система имеет решения x₁, у₁, z₁ Укажите симметричное решение, которое наряду с этим будет иметь система.

9.31. Поскольку вместе с условием x + у = 0 мы получаем три уравнения с двумя неизвестными, то имеет смысл воспользоваться подстановкой у = ?x.

9.32. Поскольку данная система должна иметь решение при любом b, то, чтобы сузить область допустимых значений а, можно рассмотреть эту систему при некотором фиксированном b.

9.33. Вначале нужно использовать условие, что система должна иметь только одно решение. Второе уравнение можно рассматривать как четную функцию относительно x и у, т. е. наряду с решением x = x₁, у = у₁ оно имеет три симметричных решения: (?x₁, у₁), (x₁, ?у₁), (?x₁, ?у₁). Какое из этих решений наряду с (x₁, у₁) будет удовлетворять первому уравнению?

9.34. Второе уравнение можно преобразовать к виду

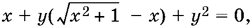
умножив числитель и знаменатель дроби на выражение, сопряженное знаменателю. Легко убедиться, что у ? 0. Поэтому можно полученное уравнение разделить на у, после чего нетрудно с помощью первого уравнения системы исключить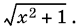

9.35. Представить уравнение в виде

|6 ? |x ? 3| ? |x + 1|| = а(x + 5) + 4,

построить график функции, стоящей в левой части равенства, и рассмотреть поведение относительно этого графика прямой у = а(x + 5) + 4 при разных значениях а.

9.36. Обе части нужно возвести в квадрат. Чтобы обеспечить равносильность, в системе с полученным уравнением придется решать неравенство 4x? ? 3аx ? 0. При этом выражение под вторым радикалом автоматически будет неотрицательным.

В задачах с параметрами, как правило, нарушать равносильность нецелесообразно. Рассуждения, связанные с ОДЗ, не дают строгого решения.

9.37. x = 0 — корень уравнения. Выражения в знаменателях имеют одинаковую составляющую 5x? + 6.

9.38. Это система однородных уравнений, и она решается стандартной подстановкой x + у = u, xу = v.