Глава 20 Суммирование
При решении задач, связанных с последовательностями, приходится доказывать утверждения такого типа: «Для любого целого n ? p (где p — целое) справедливо...»
Доказательство этих утверждений базируется на аксиоме индукции.
Пусть для некоторого утверждения А доказаны две теоремы.
Теорема 1. Утверждение А справедливо для n = p.
Теорема 2. Из условия, что утверждение А справедливо для всех p ? n ? k, следует, что оно справедливо для n = k + 1.
Тогда в качестве аксиомы (она называется аксиомой индукции) принимают, что утверждение А справедливо для всех n ? p (n, p и А — целые числа).
Метод доказательства, основанный на использовании аксиомы индукции, называется методом математической индукции.
С помощью метода математической индукции можно доказать формулы
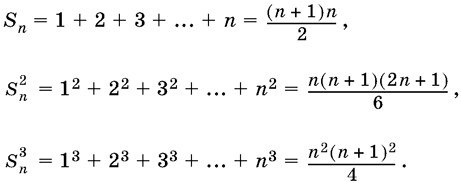
20.1. Докажите неравенство
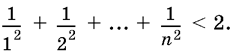
20.2. В арифметической прогрессии а1, а2, ..., аn первый член равен разности прогрессии: а1 = d. Считая число n данным, найдите
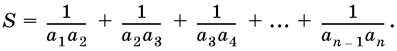
20.3. Найдите сумму
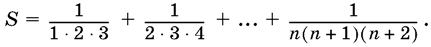
20.4. Найдите зависимость между натуральными n и А, если
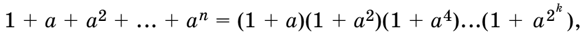
где а ? 0, 1, ?1.
20.5. Найдите коэффициент при хn в разложении
(1 + x + 2х? + ... + пхn)?.
20.6. Решите неравенство
|x ? 2х? + 4х? ? 8х4 + ... + (?2)n ? 1хn + ...| < 1.
20.7. Найдите сумму
Sn = 1 · 1! + 2 · 2! + 3 · 3! + ... + n · n!.
20.8. Найдите сумму
Sn = x + 4х? + 7х5 + 10х7 + ... + (3n ? 2)х2n ? 1.
20.9. Найдите сумму
Sn4 = 14 + 24 + 34 + ... + n4,
считая известными формулы для Sn, Sn?, Sn? (см. с. 103).
20.10. Натуральные числа разбиты на группы
(1), (2, 4), (3, 5, 7), (6, 8, 10, 12), (9, 11, 13, 15, 17), ...
Найдите сумму чисел в n-й группе.
20.11. Вычислите выражение
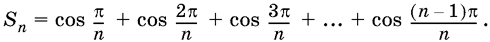
20.12. Найдите сумму
1 + 2 · 2 + 3 · 2? + ... + 100 · 299.
20.13. Найдите сумму ряда
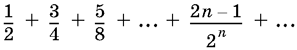
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК