K главе 4

4.1. Построение сечения, о котором идет речь в задаче, показано на рис. I.4.1. Вначале найдена точка F сечения, лежащая в плоскости нижнего основания на пересечении прямых АЕ и DС.

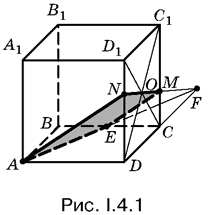
4.2. Построение сечения показано на рис. I.4.2, который подсказывает и рациональный способ вычисления площади сечения.

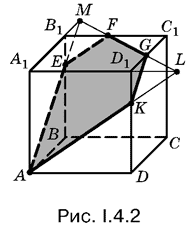
4.3. Чтобы построить сечение, проведите прямую через вершину А и центр верхнего основания и найдите точку пересечения этой прямой с ребром СС₁.

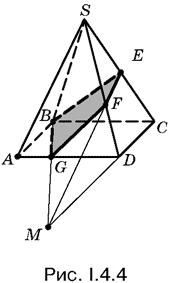
4.4. Сечение BEFG (рис. I.4.4) разбивает пирамиду на две части. Удобнее найти объем той части пирамиды, которая лежит под сечением, представив эту фигуру в виде разности двух пирамид EBCM и FGDM.

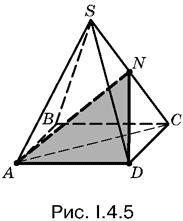
4.5. Сечение должно пройти через точки А, D и N (рис. I.4.5). Если их соединить, то получим пирамиду NACD, которую сечение отрезает от половины данной пирамиды.

4.6. Основную трудность в этой задаче представляет построение сечения. Начните с построения вспомогательного треугольника PQR.

4.7. Связать сечение с перпендикулярной к нему плоскостью центрального сечения пирамиды.

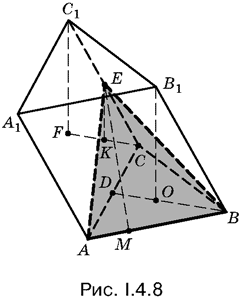
4.8. Чтобы вычислить площадь треугольника ABE, достаточно найти его высоту ЕМ (рис. I.4.8). Высоту B₁O призмы нетрудно вычислить, а высота EK пирамиды EABC в два раза меньше B₁O.

4.9. Чтобы построить сечение, достаточно провести через точку F два отрезка, лежащих внутри данного параллелепипеда: один в одной диагональной плоскости параллельно BD, а второй в другой диагональной плоскости параллельно AC₁.

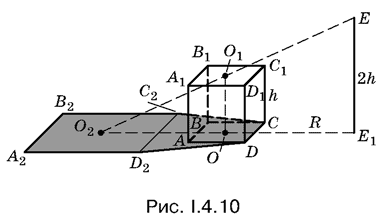
4.10. Построение тени, отбрасываемой кубом, показано на рис. I.4.10. Посмотрите, как будет изменяться тень при вращении источника света.

4.11. Площадь тени не изменится при произвольном параллельном переносе куба. Поэтому удобно расположить куб так, чтобы по крайней мере одна из его вершин (обозначим ее А) лежала в плоскости ? (рис. I.4.11).

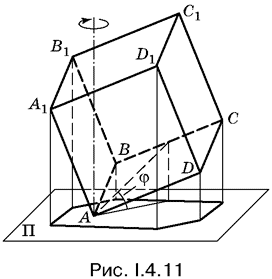
Площадь тени не изменится также и при вращении куба вокруг вертикальной прямой, проходящей через вершину А. Следовательно, для определения положения куба удобно воспользоваться острым углом между плоскостью его нижнего основания и плоскостью ?, который при таком вращении не изменяется.

Задача существенно упростится, если удастся выбрать в кубе простейшую фигуру, составленную из плоских фигур, которая отбрасывает на плоскость ? ту же самую тень.