K главе 20

20.1. Данное неравенство эквивалентно такому:

¹/_2? + ... + ¹/_n? < 1.

Оценить каждое слагаемое так, чтобы легко было оценить всю сумму, стоящую слева.

20.2. Домножить все члены на d.

20.3. Чтобы разложить дробь 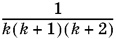 на простейшие, можно начать с разложения дроби 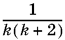, а результат умножить на .

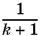20.4. Слева стоит сумма членов геометрической прогрессии.

20.5. Выписать все коэффициенты многочлена 1 + x + 2x? + ... + nxⁿ и под ними написать коэффициенты того же многочлена, записанные в обратном порядке. Рассмотреть сумму произведений стоящих друг под другом чисел.

20.6. В левой части неравенства стоит абсолютная величина суммы членов бесконечной геометрической прогрессии со знаменателем ?2x.

20.7. Каждое слагаемое k · k! можно представить в виде (k + 1)k! ? k(k ? 1)!. При этом следует иметь в виду, что 0! = 1. (!)

20.8. Коэффициенты в правой части образуют арифметическую прогрессию с разностью 3. Если домножить S_n на x?, то справа получим сумму, все члены которой, кроме крайних, имеют коэффициент, отличающийся от подобного коэффициента S_n на 3.

20.9. Рассмотреть тождество

(x + 1)⁵ = x⁵ + 5x⁴ + 10x? + 10x? + 5x + 1

и положить в нем последовательно x = 1, 2, ..., n.

20.10. В n-й группе n членов. Рассмотрите отдельно случаи, когда n четное и n нечетное.

20.11. Удобнее найти 2S_n sin ^?/_2n.

20.12. Можно разбить эту сумму на 1 00 сумм:

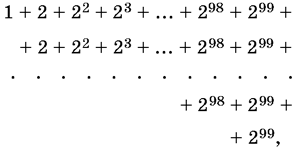
каждая из которых является суммой членов геометрической прогрессии. Однако попытайтесь решить эту задачу проще, обозначив искомую сумму через в и осуществив над ней некоторое несложное преобразование.

20.13. Общий член ряда имеет вид 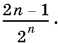 Чтобы воспользоваться формулой геометрической прогрессии, нужно избавиться от 2 n в числителе. Чтобы понять, как это лучше сделать, запишите рядом два соседних члена ряда.