K главе 24

24.1. Заменить cos? x на 1 ? sin? x. В результате получится квадратный трехчлен относительно sin x.

24.2. Записать у как одну функцию другого аргумента.

24.3. Привести к одной тригонометрической функции другого аргумента.

24.4. Выражение можно представить в виде А? + В? + С, где С — константа.

24.5. Чтобы раскрыть знаки абсолютных величин, нужно нанести на числовую ось точки ±1 и ±2, которые разобьют ее на пять интервалов.

24.6. Воспользоваться неравенством между средним арифметическим и средним геометрическим нескольких чисел.

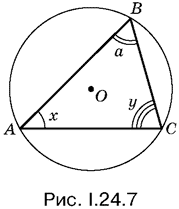
24.7. Чтобы найти максимум AB + BC, удобно ввести углы x и у (рис. 1.24.7), имея в виду, что x + у = ? ? ?, и перейти с помощью теоремы синусов к тригонометрическим соотношениям. (!)

24.8. Если обозначить катеты основания через а и b, то боковая поверхность призмы равна

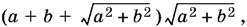
причем ab = 4.

24.9. Квадрат должен быть вписан в шестиугольник так, чтобы не нарушалась симметрия, т. е. центр квадрата должен совпадать с центром шестиугольника.

24.10. Прежде всего необходимо обратить внимание на свойства квадратного трехчлена, стоящего в знаменателе. Его дискриминант отрицателен и, следовательно, трехчлен не может быть равен нулю при действительных x.

Если обозначить теперь данную дробь через у, то можно получить квадратное уравнение относительно x, в котором у играет роль параметра.

24.11. Если ребра параллелепипеда обозначить через а, b и с, то условие задачи можно записать в виде системы

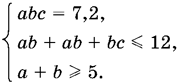
Из второго и третьего неравенств следует, что

ab + с(а + b) ? ab + 5с.

24.12. Чтобы найти наименьшее значение этой функции, естественно выделить полный квадрат. Однако удобнее вначале перейти от котангенсов к косекансам, что позволяет выразить функцию только через синусы:

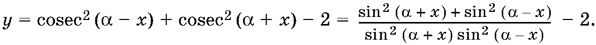
Теперь в числителе следует выделить полный квадрат разности. При этом могут представиться два случая, в зависимости от знака произведения sin (? + x) sin (? ? x). Чтобы не рассматривать их отдельно, можно необходимые преобразования записать так:

sin? (? + x) + sin? (? ? x) = [|sin (? + x)| ? |sin (? ? x)|]? + 2 |sin (? + x) sin (? ? x)|.

24.13. Известно, что arcsin x + arccos x = ^?/₂ . Поэтому данную функцию удобно преобразовать так, чтобы воспользоваться этим соотношением.

24.14. Воспользоваться преобразованием нормирования:

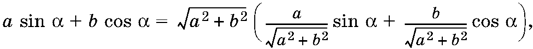
после чего коэффициенты при sin ? и cos ? можно объявить косинусом и синусом общего аргумента ?, т. е.

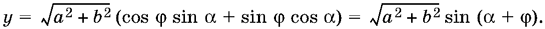
Функция у достигает своего наименьшего значения

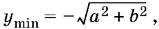
когда sin (? + ?) = ?1, и наибольшего значения

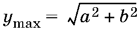
при sin (? + ?) = 1. (!)

24.15. Систему естественно привести к виду

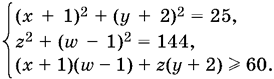
Свободные члены равны, соответственно, 5?, 12? и 5 · 12. Удобно каждое из соотношений разделить на его свободный член.