K главе 6

6.1. Воспользоваться тождеством p? ? 1 = (p ? 1)(p + 1).

6.2. Способ 1. Воспользоваться методом математической индукции. (!)

Способ 2. Разбить все числа на классы по модулю 3:

n = 3k, n = 3k + 1, n = 3k ? 1,

и проверить утверждение для каждого класса. (!)

6.3. Поскольку 105 = 3 · 5 · 7, то а¹⁰⁵ = (а?)³⁵ = (а⁵)²¹ = (а⁷)¹⁵. Воспользуйтесь этим для разложения данного числа на множители.

6.4. Среди чисел от 1 до 500 будет 250 четных, 125 делящихся на 4 и т. д.

6.5. Чтобы данное число приняло более симметричный вид, его удобно умножить на 10. При этом делимость его на 81 не изменится.

6.6. Дополнить выражение n⁴ + 4 до полного квадрата и разложить на множители.

6.7. Так как по условию n четное, то нужно сделать подстановку n = 2k и привести данное выражение к общему знаменателю.

6.8. Способ 1. Дробь 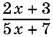 сократима тогда и только тогда, если ее числитель представим в виде pr, а знаменатель — в виде qr, где p, q и r — целые числа и r ? ±1.

Способ 2. Если сократима дробь ^p/_q , то сократима и дробь ^q/_p.

6.9. Использовать сначала признак делимости на 4, а затем признак делимости на 9. (!)

6.10. Если условие, в силу которого число 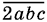 в три раза меньше  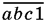записать символически, то получим уравнение, которое нужно будет решить в целых числах, каждое из которых расположено между 0 и 9.

6.11. Ясно, что число p нечетное. Одно значение p легко угадать — это p = 3. Есть ли другие?

6.12. Задачу удобнее решать от противного, исходя из предположения, что tg 5° = ^p/_q , где p и q — целые.

6.13. Если меньшее из чисел не оканчивается цифрой 9, то суммы цифр этих чисел различаются на 1. Поэтому обе суммы цифр одновременно делиться на 11 не могут. Нужно искать решение среди чисел, меньшее из которых оканчивается одной или несколькими цифрами 9.

6.14. Нужно правильно использовать условие, в силу которого x и у — целые. Однородное выражение относительно неизвестных нужно оставить слева и попытаться разложить на множители, а число 17 перенести в правую часть равенства.

6.15. Данное уравнение таково, что если x = а, у = b — его решение, то существуют еще три решения: (?а, b), (а, ?b), (?а, ?b), если а ? b.

6.16. Преобразовать исходное условие к виду 11(4x ? 1) = 69(у ? x) и воспользоваться тем, что x и у — натуральные числа.