Глава 24 Наибольшие и наименьшие значения

24.1. Так как sin x ? cos? x ? 1 = sin? x + sin x ? 2 = (sin x + ?)? ? ⁹/₄, то функция достигает своего наименьшего значения при sin x + ? = 0.

Ответ. x = (?1)^{k + 1 ?}/₆ + ?k.

24.2. Воспользуемся формулой преобразования произведения синусов

y = ?[cos ^?/₆ ? cos (4x ? ^?/₆)] = ^?3/₄ ? ?cos (4x ? ^?/₆).

Чтобы функция y достигла своего наибольшего значения, нужно положить cos (4x ? ^?/₆) = ?1, откуда x = ^?/₂₄ + ^?/₄ (2n + 1) = ^?n/₂ + ^7?/₂₄. Наибольшее значение функции равно y_max = ^?3/₄ + ?.

Ответ. При x = ^?n/₂ + ^7?/₂₄ y_max = ^?3/₄ + ?.

24.3. Данную функцию можно записать в виде y = sin x cos x (cos? x ? sin? x), после чего она легко преобразуется: 4y = 2 sin 2x cos 2x = sin 4x.

Ответ. ?.

24.4. Запишем данное выражение в виде (x + y + 1)? + (x ? 2)? ? 3. Оно будет иметь наименьшее значение, если одновременно x ? 2 = 0 и x + y + 1 = 0.

Ответ. ?3 при x = 2.

24.5. Точки ±1 и ±2 разбивают числовую ось на пять интервалов, в каждом из которых нетрудно найти наименьшее значение y.

1. Если x ? ?2, то y = x? ? 1 + x? ? 4 ? x ? 2 ? x ? 1 = 2x? ? 2x ? 8.

Абсцисса вершины параболы y = 2x? ? 2x ? 8 равна x = ?^b/_2a = ?,

т. е. при x ? 2 мы находимся левее вершины, функция y на этом участке убывает, а потому наименьшее значение она принимает в самой правой точке интервала: x = ?2, y = 4.

2. Если[23] ?2 ? x ? ?1, то легко проверить, что y = 4.

3. Если ?1 ? x ? 1, то y = ?2x? + 2x + 8.

Так как ветви параболы направлены вниз, то наименьшее значение нужно искать на концах интервала: при x = ?1 мы уже видели, что y = 4; при x = 1, y = 8.

4. Если 1 ? x ? 2, то y = 2x + 6. Наименьшим будет значение в точке x = 1.

5. Если x ? 2, то y = 2x? + 2x ? 2.

Абсцисса вершины этой параболы x = ??; она лежит левее точки x = 2. Следовательно, наименьшее значение достигается при x = 2, т. е. y = 10.

Ответ. y_min = 4 при ?2 ? x ? ?1.

24.6. Заменим ^a/_x на сумму из семи одинаковых слагаемых, каждое из которых равно ^a/_7x. К функции

x⁷ + ^a/_7x + ^a/_7x + ^a/_7x + ^a/_7x + ^a/_7x + ^a/_7x + ^a/_7x

применим неравенство между средним арифметическим и средним геометрическим 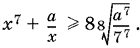 Равенство достигается при  

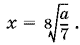
Ответ.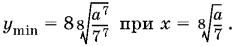

24.7. Если ввести углы x и y (рис. P.24.7), то по теореме синусов AB + BC + 2R(sin x +  sin y) = 4R sin [^{? ? ?}/₂] cos [^{x ? y}/₂].

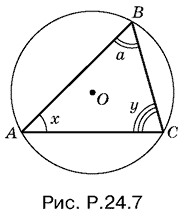
Наибольшее значение этого выражения достигается при cos [^{x ? y}/₂] = 1, т. е. при x ? y = 0. Так как x + y = ? ? ?, то x = ^?/₂ ? ^?/₂. Следовательно,

AB = ВС = 2R sin x = 2R cos ^?/₂.

Ответ. 2R cos ^?/₂.

24 . 8 . Если катеты основания обозначить через а и b, то боковая поверхность призмы равна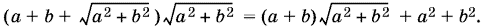

Нам известна площадь основания. Поэтому аb = 4. Преобразуем выражение для боковой поверхности так, чтобы участвовали только аb и а + b: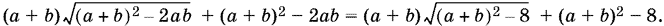

Мы получили монотонную функцию от а + b. Ее наименьшее значение достигается одновременно с наименьшим значением а + b. Поскольку а + b ? 2?ab = 4, то равенство достигается, если а = b = 2.

Ответ. 2.

24.9. Так как правильный шестиугольник и квадрат — фигуры центрально?симметричные, то центр вписанного в шестиугольник квадрата должен совпадать с центром шестиугольника. Пусть K (рис. P.24.9) — одна из вершин квадрата, а M — центрально?симметричная ей точка многоугольника.

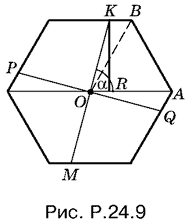
Обозначим через ? угол AOK. Тогда 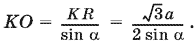 По теореме синусов 

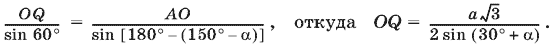
Чтобы задача имела решение, должно быть OQ ? OK, т. е. sin (30° + ?) ? sin ?. Так как угол а больше угла BOA, то ? ? 60°. Кроме того, можно считать, что ? ? 90°, т. е. 60° ? ? ? 90°. Чтобы для этих углов выполнялось условие

sin (30° + ?) ? sin ?,

необходимо и достаточно, чтобы 75° ? ? ? 90°. Из формулы для KO видно, что с увеличением ? диагональ квадрата уменьшается. Следовательно, ? нужно выбрать минимальным из возможных, т. е. ? = 75°. Тогда 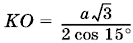, а сторона квадрата равна KO ?2.

Ответ.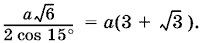

24.10. Обозначим данную дробь через y. Поскольку дискриминант квадратного трехчлена, стоящего в знаменателе, меньше нуля, уравнения

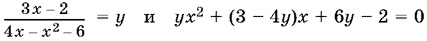
равносильны. Чтобы x было действительным числом, необходимо и достаточно выполнение условия (3 ? 4у)? ? 4у(6у ? 2) ? 0, т. е. 8у? + 16у ? 9 ? 0. Ему удовлетворяют значения y, для которых ?1 ? ^?34/₄ ? y ? ?1 + ^?34/₄. Правый конец интервала и будет наибольшим значением дроби.

Ответ. ^?34/₄ ? 1.

24.11. Пусть а, b, с — ребра параллелепипеда. Тогда ограничения, указанные в условии задачи, запишутся в виде системы трех соотношений:

аbс = 7,2, аb + ас + bс ? 12, а + b ? 5.

Преобразуем второе соотношение, приняв во внимание, что а + b ? 5:

аb + ас + bс = аb + с(а + b) ? аb + 5с,

т. е. аb + 5с ? 12. Перепишем теперь первое соотношение в виде аb · 5с = 36. Чтобы решить систему неравенства и уравнения, отыщем точки пересечения прямой x + y = 12 с гиперболой xy = 36, где x = аb, y = 5с. Решая эту систему, найдем единственную точку x = y = 6. Отсюда легко следует, что системе, записанной вначале, отвечают лишь числа с = ⁶/₅, аb = 6. Подставив эти значения во второе соотношение, получим а + b ? 5. Поскольку одновременно а + b ? 5 (третье соотношение), то а + b = 5 наряду с условием аb = 6.

Ответ. 2, 3, ⁶/₅.

24.12. Преобразуем данную функцию следующим образом:

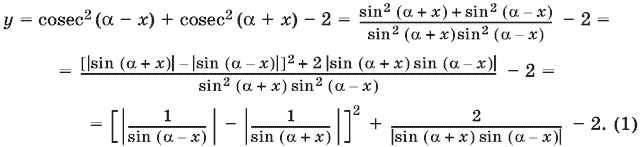
Второе слагаемое достигает своего наименьшего значения, когда его знаменатель максимален. Поскольку

|sin (? + x) sin (? ? x)| = ?|cos 2x ? cos 2?|,

то наибольшее значение этого выражения достигается при cos 2x = ?1, если cos 2? ? 0, 0 < ? ? ^?/₄, и при cos 2x = 1, если cos 2? < 0, ^?/₄ < ? < ^?/₂.

В первом случае x = ^{?(2k + 1)}/₂, во втором x = ?k. И в том и в другом случае первое слагаемое выражения (1) обращается в нуль. Следовательно, при 0 < ? ? ^?/₄ наибольшее значение функции равно 2 tg? ?, а при ^?/₄ < ? < ^?/₂ равно 2 ctg? ?.

Ответ. 2 tg? ? при 0 < ? ? ^?/₄, 2 ctg? ? при ^?/₄ < ? < ^?/₂·

24.13. Введем обозначения: arcsin x = ?, arccos x = ?. Поскольку ? + ? = ^?/₂, то

?? + ?? = (? + ?)? ? 3??(? + ?) = ^??/₈ ? ^3?/₂??.

Наименьшее значение данной функции соответствует наибольшему значению произведения ??. Так как ? ? 0, то наибольшее значение ?? следует искать при ? > 0. В этом случае (? > 0, ? > 0) можно записать, что

?? ? (^{? + ?}/₂)? = ^??/₁₆.

Наибольшее значение ?? достигается при ? = ? = ^?/₄. Следовательно, наименьшее значение исходной функции достигается при x = ¹/_?2 и равно

^??/₈ ? ^3??/₃₂ = ^??/₃₂.

Наименьшее значение произведения ??, где ? ? 0, достигается при условии, что ? < 0, причем желательно, чтобы абсолютные величины ? и ? были наибольшими. При x = ?1 будет ? = ?^?/₂, ? = ?. Именно в этой точке произведение ?? достигает минимума, так как ? принимает минимальное, а ? — максимальное из возможных значений. Итак, при x = ?1 исходная функция имеет наибольшее значение

^??/₈ + ^3?/₂ ^?/₂ ? = ^7??/₈.

Ответ. ^??/₃₂, ^7??/₈.

24.14. Сделаем следующие преобразования:

y = 2 sin? x + 2 cos? x + 4(2 cos? x) ? 2 sin 2x = 2 + 4(1 + cos 2x) ? 3 sin 2x = 6 + 4 cos 2x ? 3 sin 2x = 6 + 5(⁴/₅ cos 2x ? ³/₅ sin 2x) = (см. указание I) = 6 + 5(sin ? cos 2x ? cos ? sin 2x) = 6 + 5 sin(? ? 2x).

Поскольку min sin (? ? 2x) = ?1, то min y = 6 ? 5 = 1.

Ответ. 1.

24.15. Преобразуем данную систему к виду

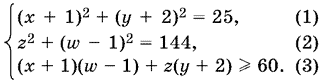
или

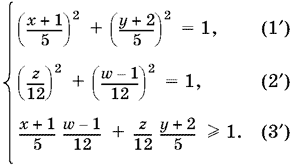
Введем новые переменные:

^{x + 1}/₅ = s, ^{y + 2}/₅ = t, ^z/₁₂ = v, ^{w ? 1}/₁₂ = u.    (4)

Тогда система примет вид

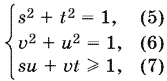
и для удовлетворяющих этой системе переменных нужно найти

min (y + w) = min (5t + 12u ? 1).   (8)

Обратим внимание на то обстоятельство, что (5) и (6) — уравнения окружностей радиуса 1. Поэтому можно положить:

s = sin ?, t = cos ?; v = sin ?, u = cos ?.

Тогда для левой части (7) получим

sin ? cos ? + sin ? cos ? = sin(? + ?) ? 1.    (9)

Учитывая соотношения (9) и (7) одновременно, получим

sin (? + ?) = 1, т. е. ? + ? = ^?/₂ + 2?k,    (10)

или

sin ? = cos ?, cos ? = sin ?,    (11)

s = u, t = v.    (12)

Соотношение (7), которое преобразуется теперь в равенство, примет вид

u? + t? = 1.    (13)

Нам нужно найти min (5t + 12u ? 1). Воспользуемся соотношениями (11) и (12), в силу которых u = sin ?, t = cos ?. Тогда st ? 12u ? 1 = 13(⁵/₁₃ ? cos ? ? ¹²/₁₃ sin? ?) ? 1 = 13 cos (? + ?) ? 1, где cos ? = ⁵/₁₃, sin ? = ¹²/₁₃. Поэтому min (5t ? 12u ? 1) = ?14.

Ответ. ?14.