К главе 13

13.1. Заменить ?2 sin (x + ^?/₄) на sin x + cos x, после чего объединить все одночлены, содержащие cos Зx, и все оставшиеся одночлены уравнения. Это поможет получить распадающееся уравнение, y которого в правой части нуль, а левая разложена на множители.

13.2. Если левую часть представить в виде 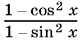, то получим распадающееся уравнение, которое нужно решать, следя за равносильностью.

13.3. Левую часть уравнения записать в виде 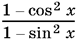, перенести все в одну часть и вынести  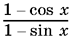за скобки. (!!)

Оставшееся в скобках выражение симметрично относительно sin x и cos x. Если привести дроби к общему знаменателю, то должно получиться достаточно простое выражение, поскольку все подобные члены будут иметь разные знаки.

13.4. Найти такие решения уравнения sin 2x sin 7x = cos 2x cos 7x, при которых cos 2x cos 7x ? 0.

13.5. Замена ctg x = ¹/_{tg x} приведет к появлению tg x множителем в числителе. Однако tg x не может быть равным нулю.

13.6. Воспользоваться формулой разности тангенсов и заменить полученное уравнение эквивалентной ему системой, состоящей из нового уравнения и ограничений.

13.7. Множитель sin (x + ^?/₄) входит в правую часть уравнения. Чтобы обнаружить это, достаточно заменить cos x на sin (^?/₂ ? x) и привести правую часть к виду, удобному для логарифмирования.

13.8. После приведения к виду, удобному для логарифмирования, внимательно следить за равносильностью.

13.9. Так как cos ^x/₂ на интервале 0 < ^x/₂ < ? меняет знак, то этот интервал придется разбить на два: 0 < ^x/₂ ? ^?/₂ , ^?/₂ < ^x/₂ < ?.

13.10. При решении получившегося уравнения нужно правильно оценить роль параметра: если из соотношения исчезает неизвестное и остается только параметр, то при данном значении параметра неизвестное может принимать любое значение из области определения данного уравнения.

13.11. Выбор значений x, попадающих в интервал 0 ? x ? 2?, удобнее осуществить, если при решении мы постараемся воспользоваться арккосинусами, областью значений которых является указанный интервал.

13.12. Под радикалом стоит полный квадрат. Помните, что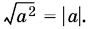

13.13. Остается заметить, что tg x + sin x = tg x(1 + cos x), а tg x ? sin x = tg x (1 ? cos x). Оба этих выражения входят слагаемыми в степени ?. Множитель tg^? x входит и в третье слагаемое. Этот множитель можно вынести за скобки, так как 1 + cos x и 1 ? cos x никогда не станут отрицательными, а следовательно, равносильность в результате этого действия не нарушится. (!!)

Получаем уравнение вида tg^? x ?(x) = 0, где ?(x) имеет смысл всегда. Это уравнение равносильно совокупности уравнения tg x = 0 и системы

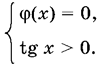
(B ограничении взято строгое неравенство, так ка случай tg x = 0 учтен раньше.)

13.14. Чтобы произвести упрощения, придется воспользоваться еще одним условным тождеством ¹/_{tg 2x} = ctg 2x. Провести анализ равносильности и перейти в полученном уравнении к синусам и косинусам.

13.15. Когда в уравнение входят только sin ? cos ? и sin ? + cos ?, то одну из этих величин, например вторую, можно обозначить через y, а другую выразить через y.

13.16. Перейти к функциям x и привести уравнение к однородному, домножив 6 sin x на тригонометрическую единицу.

13.17. Воспользоваться теоремой о рациональных корнях многочлена с целыми коэффициентами.

13.18. Выразить правую и левую части через y = cos ^x/₂.

13.19. Выражение в квадратных скобках представить в виде

(1 + ctg x) + [ 1 + ctg (^?/₄ ? x) ]

и воспользоваться формулой суммы котангенсов. B правой части для cos 2 x нужно выбрать выражение, которое позволит избавиться от стоящей в скобках единицы.

13.21. Относительно cos x получится биквадратное уравнение, решения которого придется исследовать.

13.24. Воспользоваться этой формулой еще раз, предварительно выделив выражение 1 + cos 2x, и получить распадающееся уравнение. (!!)

Вспомнить об условиях, при которых произведение двух косинусов равно единице.

13.25. Записывая условие одновременного равенства двух косинусов единице или минус единице, следует брать разные обозначения для целочисленного переменного.

13.26. Если перенести все в правую часть, то мы сможем образовать сумму двух неотрицательных слагаемых.

13.27. Так как cos 3x ? 0, а при дополнении до полного квадрата к обеим частям уравнения прибавляется ± cos x cos 3x, то знак правой части зависит от знака cos x. Это означает, что целесообразно рассмотреть три случая: cos x = 0, cos x > 0, cos x < 0. (!!)

Если cos x > 0, то целесообразно привести левую часть к квадрату разности, а если cos x < 0 — к квадрату суммы.

13.28. Поскольку минимум левой части совпадает с максимумом правой, то единственная возможность их уравнять — решить систему

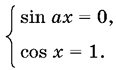
13.29. При решении окажется полезной следующая идея. Если уравнение преобразуется к виду f(x) g(x) = 0, причем корни f(x) находятся легко и содержат все корни g(x), то решать уравнение g(x) не следует. Поскольку в нашем случае уравнение f(x) g(x) = 0 было получено из системы, то остается выяснить, какие из корней уравнения f(x) = 0 приведут к решению исходной системы.

13.30. Первое уравнение можно привести к виду

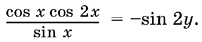
При подстановке 2y = ^?/₄ ? x + k? приходится рассматривать случаи k = 2p и k = 2p + 1.

13.31. Относительно и и v получится система уравнений, которую удобно решить заменой v = ut.

13.32. С помощью второго уравнения выразить y через x и подставить в первое уравнение системы.

13.33. При решении системы нам придется оба уравнения возводить в квадрат. Следовательно, в конце необходимо сделать проверку.

13.34. Получив из второго уравнения после подстановки в него найденного значения x выражение для |y|, нужно позаботиться о том, чтобы |y| ? 0.

13.35. Из третьего уравнения x + y = ? ? z. Следовательно, tg z = ?tg (? ? z) = ?tg (x + y). (!!)

По формуле тангенса суммы и с помощью уравнения tg y = 2tg x можно выразить tg z через tg x и подставить в первое уравнение.

13.36. Получить уравнения с одинаковыми левыми частями и сравнить их. При решении квадратного уравнения обратить внимание на исследование.

13.37. Прежде чем возводить уравнения в квадрат, оставим в левой части первого уравнения sin x, а в левой части второго уравнения оставим cos x.

13.38. При решении уравнений возникнут арксинусы и арккосинусы, которые будут накладывать ограничения на а. Следует ли к этим ограничениям добавлять |а| ? 1, |а + ?| ? 1, что вытекает непосредственно из условия?

13.39. Оценив правую и левую части уравнения, обнаружим, что равенство возможно лишь в случае, если обе равны четырем. B результате уравнение сводится к системе. B частности, следует обратить внимание на то обстоятельство, что левая часть равна 4 лишь при tg x = tg y = 1.

13.40. Способ 1. Преобразовать уравнение в сумму квадратов и заменить системой.

Способ 2. Уравнение преобразуется к сумме двух неотрицательных выражений, которая равна нулю. B результате получим систему

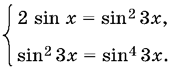
13.41. Способ 1. После преобразования данное уравнение примет вид

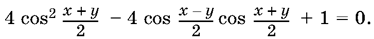
Первые два члена дополнить до полного квадрата и получить сумму неотрицательных слагаемых, которая равна нулю.

Способ 2. Уравнение можно записать в виде

(1 ? cos x) cos y + sin x sin y = ³/₂ ? cos x

и рассмотреть левую часть как однородное выражение относительно sin y и cos y. Остается оценить выражение A cos y + B sin y и правую часть уравнения.

13.42. Способ 1. Обозначив tg x = z, tg а = с, мы придем к выражению, которое должно быть тождеством относительно x. Остается вспомнить условие тождественного равенства двух многочленов.

Способ 2. Так как равенство

tg x + tg (а ? x) + tg x tg (а ? x) = b

должно выполняться тождественно, т. е. при всех x, то оно должно быть верным и для конкретных значений x, например при x = 0 и x = ^?/₄ . Найденные в результате значения а и b нуждаются в проверке.

13.43. На первый взгляд кажется естественным воспользоваться оценкой

sin? x + ¹/_{sin? x} ? 2, cos? x + ¹/_{cos? x} ? 2.

Однако это очень грубая оценка. B самом деле, если для одного из выражений достигается равенство, то другое обращается в бесконечность.

Следовательно, нужно преобразовать левую часть уравнения так, чтобы sin? x и cos? x не были разъединены. С этой целью удобно раскрыть скобки и заменить

sin⁴ x = ? (1 ? cos 2x)?, cos⁴ x = ? (1 + cos 2x)?.

13.44. Левую часть выражения

sin 2x ? sin x cos 2x = ³/₂ ,

к которому приводится данное уравнение, удобно рассмотреть как A sin 2x + B cos 2x, где А = 1, B = -sin x, и оценить.

13.45. Задача сводится к уравнению типа sin ? + cos ? = 2, которое равносильно системе: sin ? = 1, cos ? = 1.

13.46. Найдя y из квадратного уравнения, следует использовать и его выражение через x (см. указание I, с. 150). При такой замене появляется опасность приобретения посторонних корней.

13.47. Данную систему уравнений удобно переписать в виде

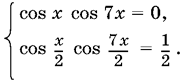
Легко заметить, что следствием полученной системы является уравнение cos 7x = 0, содержащее в качестве корней не только все числа, для которых cos x = 0, но и все корни второго уравнения. B самом деле, при cos 7x = 0 получим cos? ^7x/₂ = 1 и, следовательно, cos? ^x/₂ = ? . Остается отсеять посторонние значения x.

13.48. Левая и правая части преобразуются к виду, когда в знаменателе и в числителе появляются общие множители. Нужно следить за ограничениями, а в конце провести отбор решений.

13.49. Все ограничения можно объединить: sin 4x ? 0. Эти значения нужно исключить из решений уравнения, полученного после преобразований.

13.50. Следить за равносильностью всех преобразований. Отобрать среди корней числителя те, которые не обращают в нуль знаменатель.

13.51. Из полученных значений t нужно отбросить те, для которых sin t = 0, cos t = 0 и cos 2t = 0, а также (это будет видно в процессе преобразований) cos 2t = ?. Первые три ограничения можно объединить: sin 4t ? 0.