Глава 12 Тригонометрические преобразования

12.1. В первых квадратных скобках после упрощений получим ²/_{sin x}, вторые квадратные скобки заключают в себе выражение 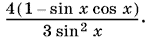Таким образом, первое слагаемое принимает вид

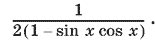
Второе слагаемое легко приводится к виду

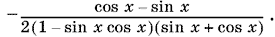
Ответ.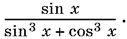

12.2. Так как сумма углов 30° ? ? и 60° ? ? равна 90° ? 2?, то

tg [(30° ? ?) + (60° ? ?)] = ctg 2?,

или

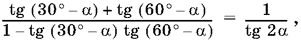
откуда следует наше тождество.

12.3. Рассмотрим выражение

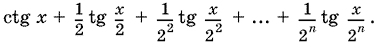
Так как ctg x = ?(ctg ^x/₂ ? tg ^x/₂),  то

ctg x + ? tg ^x/₂ = ? ctg ^x/₂.

Аналогичные преобразования можно продолжить и дальше:

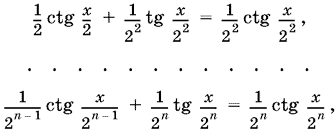
что и доказывает тождество.

12.4. Перепишем равенство

sin ? cos (? + ?) = sin ?

в виде

sin ? cos (? + ?) = sin [(? + ?) ? ?],

т. е.

sin ? cos (? + ?) = sin (? + ?) cos ? ? sin ? cos (? + ?),

или

2 sin ? cos (? + ?) = sin (? + ?) cos ?.

Из условия следует, что cos (? + ?) ? 0 и cos ? ? 0. Разделим последнее равенство на cos (? + ?) cos ?. Получим

2 tg ? = tg (? + ?).

12.5.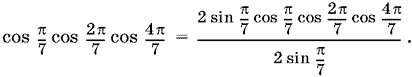

Применяя последовательно формулу синуса двойного угла, приведем числитель к виду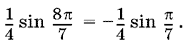

Ответ. ?¹/₈.

12.6. Вычислим вначале произведение косинусов:

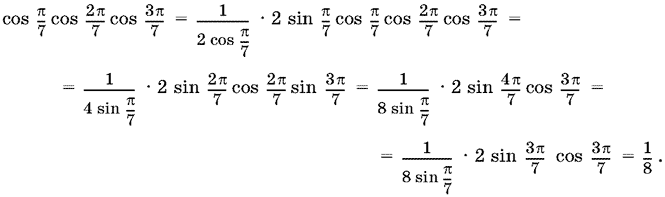
Теперь вычислим произведение квадратов синусов, умноженное на 8:

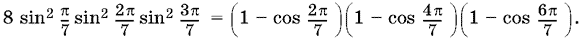
Раскроем скобки и преобразуем каждое произведение двух косинусов в сумму косинусов. После приведения подобных получим

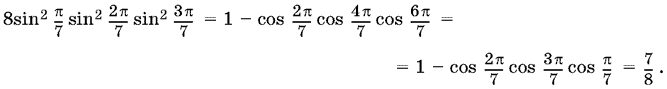
Теперь можно найти произведение тангенсов.

Ответ. ?7 .

12.7. Преобразуем правую часть равенства, которое нужно доказать:

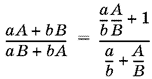
и воспользуемся условием. Получим

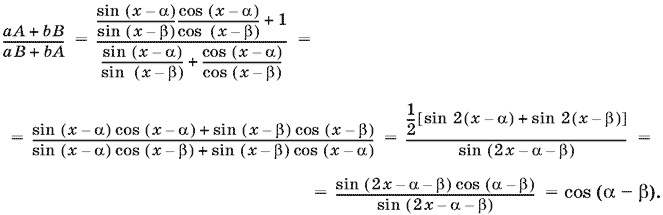
12.8. Доказательство представляет собой цепочку преобразований sin (x + y) sin (x ? y) = sin? x cos? y ? cos? x sin? y = k? sin? y cos? y ? cos? x sin? y = sin? y (k? cos? y ? cos? x).

Так как cos? x = 1 ? k? sin? y, то выражение в скобках равно k? ? 1. По условию ?1 ? k ? 1, т. е. k? ? 1 ? 0, и, следовательно, sin (x + y) sin (x ? y) ? 0.

12.9. Вычислим а? + b?:

а? + b? = 2 + 2 (cos ? cos ? + sin ? sin ?) = 2 + 2 cos (? ? ?) = 4 cos? ^{? ? ?}/₂. Теперь преобразуем правую часть равенства, которое нужно доказать:

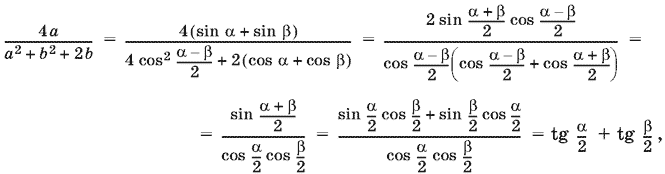
что и требовалось доказать.

12.10. Обозначим sin? ? = а, sin? ? = b, sin? ? = с. Тогда данное в условии соотношение примет вид

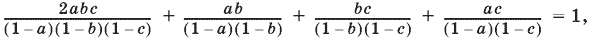
т. е.

2abс + аb(1 ? с) + bс(1 ? а) + ас(1 ? b) ? (1 ? а)(а ? b)(1 ? с) = 0.

После того как будут раскрыты скобки и приведены подобные члены, получим

?1 + с + b + a = 0,

что в первоначальных обозначениях соответствует равенству sin? ? + sin? ? + sin? ? = 1.

12.11.

При преобразованиях мы пользовались формулами преобразования произведения тригонометрических функций в сумму.

Ответ. ?3.

12.12. Так как

ctg ? + ctg ? = 2 ctg ? и ? = ^?/₂ ? (? + ?),

то

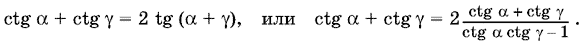
Углы ? и ? острые. Поэтому ctg ? > 0 и ctg ? > 0 и на их сумму можно сократить:

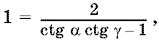
откуда легко найти произведение котангенсов.

Ответ. 3.

12.13. Преобразуем данное выражение:

sin (90° + 16°) + cos (90° + 16°) ctg 8° = cos 16° ? sin 16° ctg 8° = cos 16° ? 2 sin 8° cos 8° ^{cos 8°}/_{sin 8°} = cos 16° ? 2 cos? 8° = cos 16° ? (1 + cos 16°) = ?1.