Глава 17 Функции и их свойства

17.1. Запишем данную систему в виде

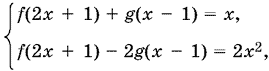
которую решим относительно f(2x + 1) и g(x ? 1):

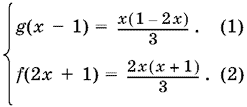
В уравнении (1) осуществим замену переменной: x ? 1 = y, т. е. x = y + 1. Тогда

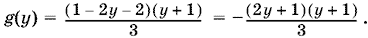
В уравнении (2) сделаем замену: 2x + 1 = z, т. е. x = ^{z ? 1}/₂. Тогда

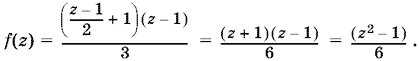
Теперь мы знаем, что

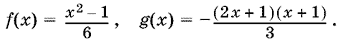
Подставим эти значения в неравенство

4f(x) + g(x) ? 0,

которое требуется решить по условию задачи. Получим

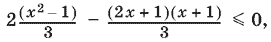
или после простых преобразований:

x + 1 ? 0, т. е. x ? ?1.

Ответ. x ? ?1.

17.2. Сначала заметим, что

f(x) = x(x? ? 6x + 9) = x(x ? 3)?.     (3)

Теперь подставим в (3) вместо x выражение f(x):

f(f(x)) = f(x)[f(x) ? 3]? = x(x ? 3)?(x? ? 6x? + 9x ? 3)?.    (4)

Уравнение f(f(x)) = 0 имеет корни x₁ = 0, x₂ = 3, а также корни уравнения

x? ? 6x? + 9x ? 3 = 0.    (5)

При всех x ? 0 значения (6) отрицательны. При всех x ? 4 значения (6) положительны. Поэтому все корни (6) лежат в интервале (0, 4). Найдем корни производной функции (6):

y? = 3x? ? 12x + 9 = 3(х? ? 4x + 3) = 3(x ? 1)(x ? 3).

При x = 1 значение y достигает максимума y = 1, а при x = 3 — минимума ?3. Следовательно, функция (6) пересекает по одному разу ось Ox на каждом из интервалов (0, 1), (0, 3), (3, 4), т. е. имеет 3 корня. Таким образом, уравнение (2) имеет 5 различных корней.

Ответ. 5.

17.3. Из второго уравнения находим

5?z = ? + 2?k, k — целое,

т. е.

z = ^{1 + 2k}/₅, k — целое.

Подставим в первое уравнение:

5 · 2^{x? ? 2xy + 1} = (1 + 2k)3^{y? ? 1}. (7)

Если y — целое, то 3^{y? ? 1} — целое при всех y ? 0. Рассмотрим вначале случай y = 0. Тогда уравнение (7) примет вид

5 · 3 · 2^{x? + 1} = 2k + 1,

и целых решений y него нет, поскольку при любых целых x слева — четное число, а справа — нечетное. Итак, y ? 0. Так как множителя 3 в левой части (7) нет, то это уравнение удовлетворяется только при y? = 1. При y = 1 получим

5 · 2^{x? ? 2xy + 1} = 2k + 1, т. е. 5 · 2^{(x ?1)?} = 2k + 1.

Левая часть последнего уравнения будет четным числом при всех целых x ? 1. Правая часть — нечетное число. Поэтому есть единственная возможность x = 1, а k = 2.

Получим решение: x = 1, y = 1, z = 1.

При y = ?1 придем к уравнению

5 · 2^{(x + 1)?} = 2k + 1,

которое удовлетворяется только при x = ?1 и k = 2. Находим еще одно решение системы: x = ?1, y = ?1, z = 1.

Других решений y системы нет.

Ответ. (1, 1, 1), (?1, ?1, 1).

17.4. Неравенство

|x + 2| ? x + 2

имеет решение x ? ?2.

Обозначим

2^{x ? 1} = y, sin ^?x/₂ = z.   (8)

Тогда уравнение, входящее в систему, примет вид

(4у + y + ¹/_y)z + (1 ? 2z?) = 3 + 2y?,

а после простых преобразований

2z? ? (5у + ¹/_y)z + 2(1 + y?) = 0.   (9)

Дискриминант уравнения (9), квадратного относительно z, равен:

D = (5у + ¹/_y)? ? 16(1 + y?) = 9у? ? 6 + ¹/_y? = (3у ? ¹/_y)?.

Поэтому решениями уравнения (9) будут:

z₁ = ?[5у + ¹/_y ? (3y ? ¹/_y)] = ?(y + ¹/_y),   (10)

z₂ = ?[5у + ¹/_y + (3у ? ¹/_y)] = 2y.

Из (8) следует, что y > 0. Из неравенства, связывающего среднее арифметическое и среднее геометрическое двух положительных чисел, при y > 0 вытекает неравенство: y + ¹/_y ? 2. Однако z = sin ^?x/₂, т. е. |z| ? 1. Но

z₁ = ?(y + ¹/_y).

Поэтому одновременно |z₁| ? 1 и z₁ ? 1, т. е. имеется единственная возможность z₁ = 1, что достигается при y = 1, а следовательно, при x = 1. Подставим значение x = 1 в исходную систему и убедимся, что это ее решение.

Для z₂ получим

sin ^?x/₂ = 2^x, где x ? ?2.    (11)

При x > 0 решений уравнение (11) не имеет, поскольку тогда 2^x > 1, а |sin ^?x/₂| ? 1.

Значение x = 0 тоже решением не является, в чем убеждаемся непосредственной проверкой.

Когда ?2 ? x < 0, решений тоже нет, так как при этих x значения 2^x положительны, а значения sin ^?x/₂ ? 0.

Ответ. x = 1.

17.5. Первообразная F(x) для функции f(x) = 6х? + 2x + 6 равна:

F(x) = 2x? + x? + 6х + С,   (12)

где константа С будет определена. Соответственно

f?(x) = 12x + 2.    (13)

В точке касания x₀ > 0,7 должны иметь место следующие соотношения:

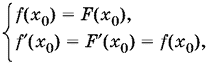
т. е. получаем систему

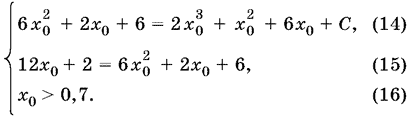
Уравнение (15) после упрощений принимает вид

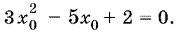
Из его двух корней x₀ = ? и x₀ = 1 условию (16) удовлетворяет только второй. Подставляем x₀ = 1 в уравнение (14) и находим, что С = 5. Окончательно

F(x) = 2x? + x? + 6х + 5.

Остается сформировать данное в условии задачи неравенство

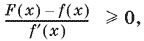
которое примет вид

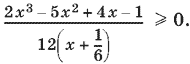
Разложим числитель на множители

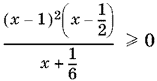
и воспользуемся методом интервалов (рис. P.17.5). Ограничение x > 0,7 относилось только к расположению точки касания графиков f(x) и F(x). Здесь его учитывать не нужно.

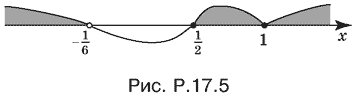
Ответ. x ? (??; ?¹/₆) ? [?; +?).

17.6. По условию разность x ? y такова, что может быть основанием логарифма. Поэтому возможна замена 1 = log_{x ? y} (x ? y), а данное в условии неравенство равносильно такому:

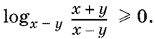
Так как (x ? y) — основание логарифма, то либо 0 < x ? y < 1, либо x ? y > 1. Получим совокупность двух систем, которую затем несколько преобразуем, чтобы удобнее было перейти к графическим изображениям:

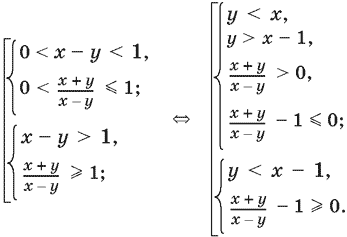
Последние два неравенства первой системы можно упростить, поскольку имеет место условие x ? y > 0. Получим

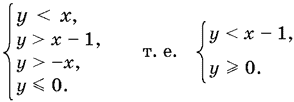
Решение первой системы показано на рис. P.17.6, а, решение второй — на рис. P.17.6, б, а решение совокупности — на рис. P.17.6, в.

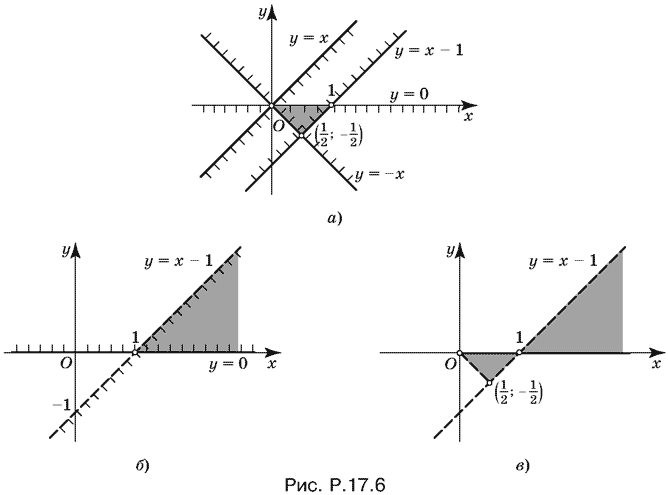
Внимание! Интервалы оси абсцисс (0, 1) и (1, +?) принадлежат множеству решений. Остальные точки границы ему не принадлежат.

17.7. Найдем решения неравенства

(x ? |x|)? + (y ? |y|)? ? 4    (17)

для каждого квадранта отдельно.

Пусть одновременно x ? 0, y ? 0. Тогда |x| = x, |y| = y. Неравенство (17) приобретет вид 0 ? 4, т. е. оно удовлетворяется при всех x и y из первого квадранта.

Когда x ? 0, y ? 0, точки (x, y) лежат во втором квадранте и на его границе. Тогда |x| = ?x, |y| = y и неравенство (17) приобретет вид

(2x)? ? 4, т. е. x? ? 1, или ?1 ? x ? 0,

так как мы рассматриваем значения x ? 0. Это будет полоса шириной 1, расположенная во втором квадранте параллельно оси Оу (рис. P.17.7).

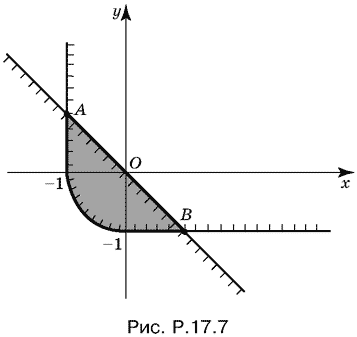
Аналогично в четвертом квадранте получим полосу шириной 1 параллельную оси Ox.

В четвертом квадранте x ? 0, y ? 0 и мы получим из (17) неравенство

х? + y? ? 1,

т. е. ему удовлетворяют точки четвертого квадранта, лежащие внутри и на границе круга x? + y? = 1.

Нанесем на рис. P.17.7 точки прямой y = ?x. Значения, удовлетворяющие неравенству x + y ? 0, будут лежать под этой прямой и на ней. Нас интересует площадь фигуры, покрытой штриховкой. Эта фигура состоит из двух прямоугольных треугольников с катетами 1 (в сумме они образуют квадрат со стороной 1) и четверти круга, имеющего радиус 1.

Ответ. 1 + ^?/₄.

17.8. Уравнение прямой, проходящей через точки В и D, имеет вид y = 8 ? x, а уравнение прямой AC есть 2y = x + 4. Решая эти два уравнения в системе, найдем x = y = 4, т. е. E(4; 4).

Проведем все построения, описанные в указании II на с. 201 (рис. P.17.8).

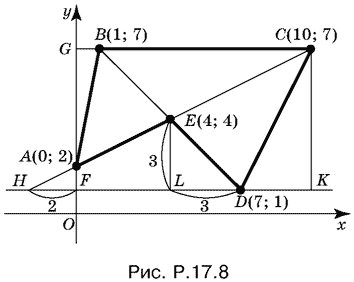
Дополнительно проведем ЕL || CK, где L ? HK, CK ? HK, F — точка пересечения HK и Оу. Искомая площадь может быть определена так:

S_ABCDE = S_FGCK ? S_CKD ? S_ELD ? S_ELH + S_AFH ? S_AGB.

Каждый из треугольников — прямоугольный с известными катетами.

Ответ. 36.

17.9. Пусть x + y = u, y ? x = v. Тогда

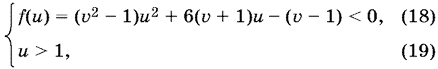
а множество решений этой системы проецируется на прямую u = 2. Другими словами, нас интересуют все значения v, при каждом из которых система неравенств (18), (19) имеет хотя бы одно решение. Пусть u — независимая переменная. Она будет абсциссой, а f(u) — ординатой для исследуемой нами плоскости. Величина v — параметр. График функции f(u) — парабола, если v? ? 1 ? 0. Она обращена ветвями вверх при v? ? 1 > 0 и ветвями вниз при v? ? 1 < 0. Отдельно нужно рассмотреть случай v? ? 1 = 0.

Итак, перед нами три случая.

1. v? ? 1 < 0, т. е. ?1 < v < 1. Парабола обращена ветвями вниз. При достаточно больших значениях u > 1 она принимает отрицательные значения. Поэтому в плоскости (u, v) в проекции на прямую u = 2 мы получим интервал ?1 < v < 1.

2. v? ? 1 = 0. Если v = ?1, то f(u) ? 2 и отрицательных решений нет. Если v = 1, то f(u) = 12u, где u > 1. Отрицательных значений, удовлетворяющих системе (18), (19), в этом случае тоже нет.

3. Когда v? ? 1 > 0, т. е. либо v < ?1, либо v > 1 ветви параболы обращены вверх. Правее прямой u = 1 парабола может принимать отрицательные значения в двух случаях:

а) уравнение f(u) = 0 имеет два корня, и при этом абсцисса u₀ вершины (u₀; v₀) параболы превосходит 1, т. е.

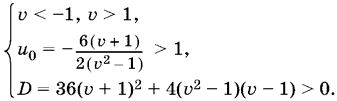
После простых преобразований:

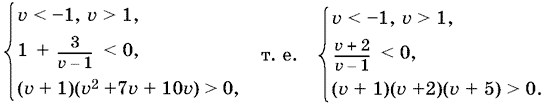
Окончательно получим

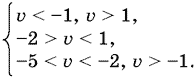
Система не имеет решений, так как одновременно все три ограничения не удовлетворяются;

б) абсцисса u₀ вершины (u₀; v₀) не больше 1, но f(1) меньше нуля:

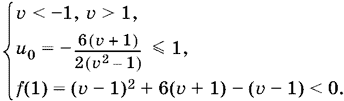
После преобразований получим

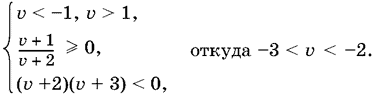
Обобщим все рассмотренные варианты. Условиям удовлетворяют два интервала значений v, проекции которых в плоскости (u, v) на прямую u = 2 не пересекаются:

v ? (?3, ?2) ? (?1, 1).

Когда мы вернемся к переменным x и y, ситуация не изменится, так как замена

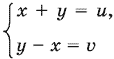
не ведет к изменению расстояний между соответственными точками в старой и новой системе координат.

Основная трудность этой задачи состояла в том, что исследование пришлось вести одновременно в двух плоскостях (u, f(u)) и (u, v). К тому же, в конечном счете, нас интересует третья плоскость (x, y).

Ответ. 2.

17.10. Если x₁ и x₂ — целочисленные корни данного уравнения, то x₁ + x₂ = а + 3, откуда следует, что а = x₁ + x₂ ? 3 — целое число. Корни данного уравнения равны

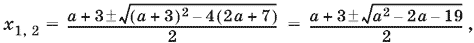
отсюда

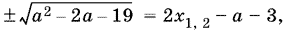
т. е. 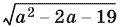 — целое число. Тогда

а? ?2a + 1 = п? + 20, т. е. (а ? 1)? ? п? = 20,

или

(а ? n ? 1)(а + n ? 1) = 20.

Остается рассмотреть варианты, когда каждая из скобок равна целочисленным множителям числа 20. Начнем со случая

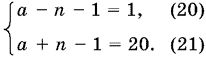
Сложив эти два уравнения, получим уравнение

2a ? 2 = 21,

не имеющее целочисленных решений.

Можно сделать более общий вывод: если в правой части других пар уравнений типа (20) и (21) есть один нечетный множитель числа 20, то целочисленных решений y системы аналогичной (20), (21) нет. Остается рассмотреть только случаи

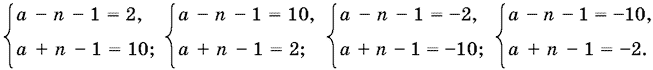
Нетрудно убедиться, что первая и вторая системы приводят к одному значению а = 7, а третья и четвертая — к значению а = ?5.

При а = 7 имеем x₁ = 3, x₂ = 7.

При а = ?5 получим x₁ = ?3, x₂ = 1.

Ответ. ?5; 7.

17.11. Обозначим x? = y, где y ? 0. Получим квадратное уравнение

y? ? (1 ? 2a)y + а? ? 1 = 0, (22)

дискриминант которого D = 5 ? 4a.

Если 5 ? 4a < 0, т. е. а > ⁵/₄, решений нет.

Если 5 ? 4a = 0, т. е. а = ⁵/₄, получим уравнение

y? + ³/₂y + ⁹/₁₆ = 0

с единственным корнем y = ??. Однако y ? 0 и потому решений тоже нет.

Пусть теперь а < ⁵/₄ и D > 0. Тогда уравнение (22) имеет корни:

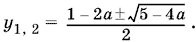
Рассмотрим сначала случаи, когда один из этих корней равен нулю, т. е.

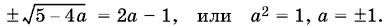
При а = ?1 получим уравнение

y? ? 3y = 0, т. е. y₁ = 0, y₂ = 3.

Поэтому при а = ?1 исходное уравнение имеет три корня 0; ??3; ?3.

При а = 1 получим

y? + y = 0,   т. е.   y₁ = 0, y₂ = ?1.

Поскольку y ? 0, то при а = 1 остается одно решение x = 0.

Теперь осталось рассмотреть два случая:

y₁ > 0 и y₂ > 0.

В первом случае нужно решить неравенство

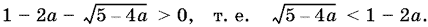
Оно равносильно системе

0 < 5 ? 4a < (1 ? 2a)?

(слева строгое неравенство, так как имеет место условие а < ⁵/₄), т. е.

0 < 5 ? 4a < 1 ? 4a + 4a?.

Правое неравенство дает нам а? > 1. Таким образом, для y₁ > 0 получим

а < ?1, 1 < а < ⁵/₄.

Для y₂ > 0 получим

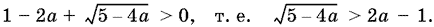
Если 2a ? 1 < 0, т. е. а < ?, то условие а < ⁵/₄ соблюдается. Поэтому при а < ? получим, что у₂ > 0. Если же 2a ? 1 ? 0, т. е. а > ?, то учтем условие а < ⁵/₄. Возведя неравенство в квадрат, получим а? < 1, т. е. во втором случае (а ? ?) получим ? ? а < 1. Окончательно у₂ > 0 при а < 1.

Объединим решения для y₁ > 0 и у₂ > 0, нанеся их на числовую прямую, учтем результат, полученный для а = ⁵/₄ (рис. P.17.11).

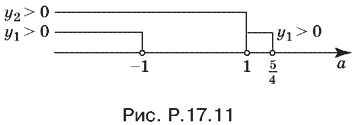
Ответ. При а < ?1 уравнение относительно x имеет четыре решения. При а = ?1 y него три решения, при ?1 < а < 1 два решения, при а = 1 одно решение, при 1 < а < ⁵/₄ два решения, при а ? ⁵/₄ решений нет.

17.12. Пусть sin 4x = y. Тогда данное уравнение преобразуется в квадратное

(a + 3)y? + (2a ? 1)y + (a ? 2) = 0,   (23)

где

|y| ? 1.   (24)

Уравнение (23) имеет решения тогда и только тогда, когда его дискриминант неотрицателен, т. е.

D = (2a ? 1)? ? 4(a + 3)(a ? 2) = 25 ? 8a ? 0.    (25)

Кроме того, нужно обеспечить, чтобы по крайней мере один из корней t₁ или t₂ уравнения (24) не превосходил по абсолютной величине 1.

Пусть сначала D = 0, т. е. а = ²⁵/₈. Тогда

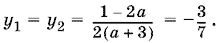
Условие (24), как мы видим, соблюдается, и уравнение sin 4x = ?³/₇ имеет решение.

Уравнение sin z = ?³/₇ на отрезке [??, ?] имеет ровно два решения z₁ и z₂. Если осуществить замену переменной: z = 4x, то отрезок [??, ?] сузится для новой переменной x в четыре раза к началу отсчета и станет отрезком [?^?/₄, ^?/₄]. Поэтому на отрезке [??, ?] для переменной x разместятся уже не 2, а 8 решений (в силу того, что sin z имеет период 2?, а sin 4x имеет период ^?/₂). Итак, а = ²⁵/₈ — одно из искомых нами значений параметра а.

Пусть теперь D > 0, т. е. а < ²⁵/₈. Тогда уравнение (23) имеет два действительных решения y₁ и y₂, такие, что y₁ < y₂. Если оба значения y₁ и y₂ попадают внутрь интервала (?1, 1), то каждому значению синуса будут соответствовать два значения переменной z в интервале (??, ?) и восемь значений переменной x = ^z/₄ в том же интервале. Решений будет ровно 8, если одно решение уравнения лежит в (?1, 1), а другое — вне этого интервала (случаи, когда y = ±1 будут рассмотрены отдельно). Конечно, можно перебрать все возможные варианты расположения y₁ и y₂ относительно интервала (?1, 1). Но это хлопотно и поэтому задачу следует упростить. Нас интересуют все случаи, когда один корень параболы, определяемой левой частью уравнения (23), внутри интервала (?1, 1), а другой вне этого интервала, т. е. парабола

f(y) = (а + 3)y? + (2a ? 1)y + (а ? 2)    (26)

пересекает интервал (?1, 1) в одной и только в одной точке. Это условие равносильно такому

f(?1)f(1) < 0,    (27)

т. е. на концах интервала (?1, 1) парабола имеет противоположные знаки. Подставим в (27) значения y = ?1 и y = 1. После преобразований получим

а < 0.

При этом условии удовлетворяется и требование D > 0, т. е. требование а < ²⁵/₈. Итак, все значения а ? (??, 0) удовлетворяют условиям задачи, как и найденное ранее значение а = ²⁵/₈. Мы не рассмотрели только случаи, когда корни уравнения (23) равны ?1 и 1.

Начнем со случая y₁ = ?1, y₂ = 1, т. е. f(?1) = f(1) = 0.

Так как f(?1) = 2, f(1) = 4a, то этот случай невозможен. Невозможен и случай, когда f(?1) = 0, так как f(?1) = 2. Остается последняя возможность: f(1) = 0. Но f(1) = 4a . Поэтому а = 0. Уравнение (23) примет вид

3y? ? y ? 2 = 0.    (28)

Уравнение (28) имеет два корня:

у₁ = ?? и y₂ = 1.

Первому из них уже будут соответствовать два значения z и восемь значений x на отрезке [??, ?]. Сколько соответствует второму, не существенно. Достаточно, что не меньше одного. Поэтому этот случай не дает новых значений параметра а.

Ответ. а ? (??, 0) ? (²⁵/₈).

17.13. Через точку на плоскости (x; y) с фиксированными координатами x и y проходит кривая семейства тогда и только тогда, когда существует значение параметра а, удовлетворяющее данному уравнению кривых семейства при этих фиксированных x и y.

Другими словами, если мы запишем уравнение семейства кривых как уравнение относительно а, то оно имеет решение при тех и только тех значениях x и y, при которых через точку плоскости с этими координатами проходит кривая семейства. Поэтому преобразуем исходное уравнение к виду

2a? + 2(x ? 2)а + (x ? 1)? ? y = 0

и потребуем, чтобы дискриминант этого уравнения был неотрицателен

D = ?х? + 2 + 2y ? 0,

откуда

y ? ^x?/₂ ? 1.

Это необходимое и достаточное условие того, чтобы через точку (x; y) проходила по крайней мере одна кривая данного семейства.

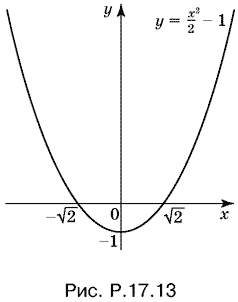
Таким образом, через все точки (x; y), лежащие вне части плоскости, ограниченной параболой y = ^x?/₂ ? 1 (рис. P.17.13), кривые семейства не проходят. Через остальные точки кривые проходят.