K главе 8

8.1. Поскольку выражения, стоящие в скобках, расположены симметрично относительно значения x = 5, удобно ввести новое неизвестное у = x ? 5. После того как мы раскроем скобки, произойдут значительные упрощения. (!)

8.2. Можно перемножить скобки по две, чтобы получить квадратные трехчлены, отличающиеся только свободным членом.

8.3. Если записать уравнение в виде x? ? 17 = 3у?, то возникает мысль доказать, что левая часть ни при каких целых x не делится на 3. (!)

8.4. Если целое у зафиксировать, то получим квадратное уравнение относительно x. Поэтому естественно обратить внимание на те ограничения, которые накладывает на у условие неотрицательности дискриминанта этого уравнения. (!)

8.5. Остаток следует искать в виде аx + b, а частное удобно обозначить через Q(x). Следуя определению деления, записать тождество.

8.6. Если переписать уравнение в виде

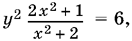
то благодаря условию целочисленности решений можно ограничить возможные значения у рассмотрением нескольких случаев.

8.7. Если подставить известный корень в уравнение, найти коэффициенты при рациональной и иррациональной частях, то получим систему двух уравнений для определения а и b.

8.8. Ответьте на вопрос: достаточно ли воспользоваться теоремой Виета, в силу которой свободный член и второй коэффициент должны быть положительными?

8.9. Если обозначить первый корень через x₁, а знаменатель прогрессии через q, то останется применить теорему Виета. (!)

8.10. С помощью теоремы Виета получить зависимость между ?₁, ?₂, ?₃ и коэффициентами данного уравнения. (!)

8.11. Разделить x? + аx + 1 на x ? ? по правилу деления многочлена на двучлен.

8.12. Ясно, что остаток нужно искать в виде аx + b. Если данный многочлен обозначить через P(x), а частное от его деления на (x ? 2)(x ? 3) — через Q(x), то мы сможем воспользоваться определением деления многочленов.

8.13. Если многочлен x⁴ + 1 разделится на x? + рx + q, то в частном мы получим многочлен второй степени, т. е. x? + аx + b.

8.14. Если данный многочлен делится на (x ? 1)?, то после замены x ? 1 = у получим многочлен, который должен делиться на у?.

8.15. Если многочлен четвертой степени с коэффициентом 6 при старшем члене делится на x? ? x + q без остатка, то в частном обязательно получится многочлен 6x? + аx + b, в котором а и b определяются одновременно с p и q.