K главе 17

17.1. Данную систему решить относительно f(2x + 1) и g(x ? 1).

17.2. f(x) = x(x? ? 6x + 9) = x(x ? 3)?,

f(f(x)) = f(x) (f(x) ? 3)? = x(x ? 3)?(x? ? 6x? + 9x ? 3)?.

17.3. Из второго уравнения найти 2 и подставить в первое. Воспользоваться условием, что x и у — целые числа.

17.4. Неравенство |x + 2| ? x + 2 удовлетворяется при всех x ? ?2.

Уравнение следует преобразовать с помощью подстановки

2^{x ? 1} = у,  sin ^?x/₂ = 2.

17.5. Найти первообразную F(x) и воспользоваться условием касания графиков функций f(x) и F(x) в некоторой точке F₀(x₀; у₀).

17.6. Данное неравенство равносильно такому:

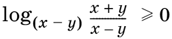
Рассмотрите случаи: а) 0 < x ? у < 1 и б) x ? у > 1.

17.7. Изобразите на графике часть плоскости, координаты точек которой удовлетворяют первому неравенству, для каждого квадранта отдельно. Для первого квадранта это будут все его точки.

17.8. Начать нужно с определения координат точки E. Для этого придется записать уравнение прямой, проходящей через две точки (x₁, у₁) и (x₂, у₂):

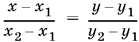
сначала для точек В и D, затем для точек А и C. Решение системы этих двух уравнений даст нам координаты точки E.

17.9. Оба неравенства зависят от x + у и от у ? x. Это подсказка побуждает ввести новые переменные u = x + у и v = у ? x.

17.10. Если x₁ и x₂ — целые, то и а — целое. (Докажите.)

17.11. Это биквадратное уравнение, и оно сводится к квадратному подстановкой x? = у. Знак дискриминанта квадратного уравнения не позволяет ответить на вопрос о числе корней исходного уравнения. Нужно позаботиться, чтобы у ? 0.

17.12. Поскольку cos 8x = 1 ? 2 sin? 4x, исходное уравнение преобразуется в квадратное относительно у = sin 4x, где |у| ? 1.

17.13. Подставив любые значения x и а в данное уравнение, получим соответствующее единственное значение у. Таким образом, при любом фиксированном а любая прямая, параллельная оси у, пересечет кривую семейства, соответствующую этому а, в единственной точке. Это не означает, что через каждую точку плоскости (x, у) проходит кривая семейства. Не при любом у мы найдем точки плоскости (x, у), соответствующие данному семейству.