Глава 22 Обратные тригонометрические функции
22.1. Введем обозначения:
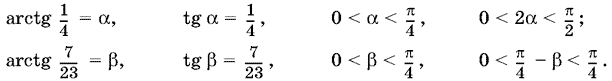
В этих обозначениях равенство примет вид
2? = ?/4 ? ?,
причем правая и левая части лежат в интервале (0, ?/2). Возьмем тангенсы от каждой из частей:
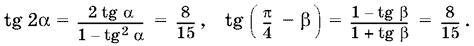
Так как тангенс является монотонной функцией в интервале (0, ?/2), то равенство доказано.
22.2. Пусть
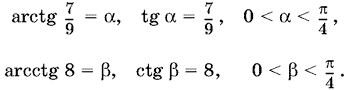
Так как 0 < ? + ? < ?/2 и
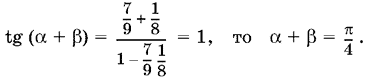
Наше выражение принимает теперь вид
?/4 + arcsin ?2/4.
Поскольку arcsin ?2/4 > arcsin ?2/2, то
0 < ?/4 + ? < ?/2,
где ? = arcsin ?2/4 и sin ? = ?2/4. Найдем
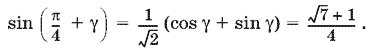
Поскольку мы оказались в интервале монотонности синуса, то остается воспользоваться определением арксинуса.
Ответ. arcsin [?7 + 1/4].
22.3. Рассмотрим сначала первое и третье слагаемые:
arctg (?2) = ?, tg ? = ?2, ??/2 < ? < 0;
arctg (??) = ?, tg ? = ??, ??/2 < ? < 0.
Таким образом, ?? < ? + ? < 0, что не является областью главных значений какой?нибудь обратной тригонометрической функции. Поэтому прибавим ко всем частям неравенства ?: 0 < ? + ? + ? < ?. Теперь ? + ? + ? попадет в область значений арккотангенса, что обеспечивает взаимно однозначный переход к обратным функциям. Найдем
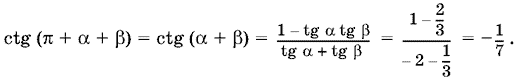
Следовательно,
? + ? + ? = arcctg (?1/7), т. е. ? + ? = ?arcctg 1/7.
Наше выражение равно arcsin ? ? arcctg 1/7. Пусть
arcsin ? = ?, sin ? = ?, 0 < ? < ?/2;
arcctg 1/7 = ?, ctg ? = 1/7, 0 < ? < ?/2.
Так как ??/2 < ? ? ? < ?/2, что является интервалом значений арксинуса, то вычислим синус от ? ? ?:
sin (? ? ?) = sin ? cos ? ? cos ? sin ?.
Так как
cos ? = 2?2/3, cos ? = 1/5?2, sin ? = 7/5?2,
то
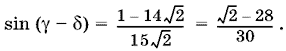
Ответ. arcsin ?2 ? 28/30.
22.4. Сумма существует при 0 ? x ? 1. Введем обозначения и используем определение арксинуса:
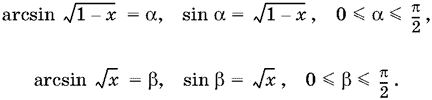
Так как сумма ? + ? лежит в интервале [0, ?], который является интервалом монотонности косинуса, то имеется взаимно однозначное соответствие между ? + ? и cos (? + ?) при условии, что 0 ? x ? 1. Так как
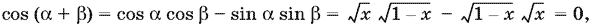
то ? + ? = ?/2.
Ответ. ?/2 при 0 ? x ? 1.
22.5. Оценим ? = ?(x? + x ? 3), если 0 ? x ? ?3 ? 1/2.
Имеем
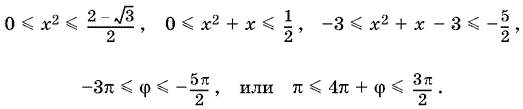
Следовательно,
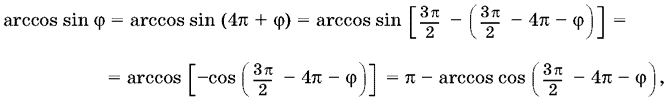
где 0 ? 3?/2 ? 4? ? ? ? ?/2. Окончательно получаем
arccos sin ? = ? ? 3?/2 + 4? + ? = 7?/2 + ?.
Ответ. 7?/2 + ?(x? + x ? 3).
22.6. При 0 ? x ? 1 оба арксинуса существуют. Для первого это очевидно, а для второго имеем
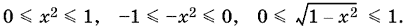
Следовательно,
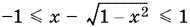
и, тем более,
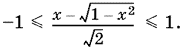
Введем обозначение
arcsin x = ?, sin ? = x, 0 ? ? ? ?/2;
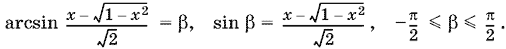
Нужно доказать, что ? ? ? = ?/4, или ? ? ?/4 = ?. Так как ??/4 ? ? ? ?/4 ? ?/4, то ? ? ?/4 и ? лежат в интервале монотонности синуса. Поэтому, если мы докажем, что синусы этих аргументов равны, то тем самым будет доказано и равенство самих аргументов. Поскольку
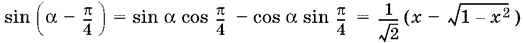
(перед корнем взят знак плюс, так как cos ? ? 0 при 0 ? ? ? ?/2).
Итак, доказано, что sin (? ? ?/4) = sin ?, откуда следует справедливость нашего равенства.
22.7. Так как x < ?1, то ?1 < 2x/1 + x? < 0. Введем обозначения
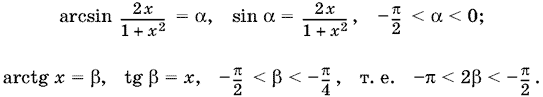
Следовательно,
?3?/2 < ? + 2? < ??/2,
т. е. данное выражение лежит в интервале монотонности синуса. Найдем
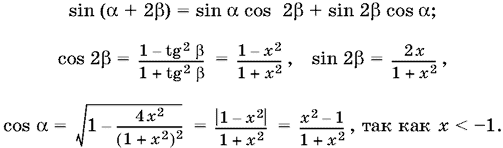
После подстановки получим
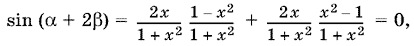
т. е. ? + 2? = ??.
Ответ. ??.
22.8. Из уравнения следует, что
arcsin x = ?/12 + n?/3.
Поскольку ??/2 ? arcsin x ? ?/2, то возможны лишь три значения n = 0, ?1, 1.
Если n = 0, то arcsin x = ?/12,
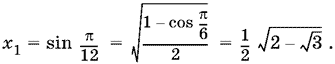
Если n = ?1, то arcsin x = ??/4,
x2 = sin (??/4) = ?1/?2.
Если n = 1, то arcsin x = 5?/12,
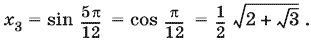
Ответ.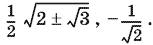 
22.9. Если x — корень данного уравнения, то и ?x будет его корнем. Поэтому достаточно найти лишь неотрицательные корни. Если x ? 0, то
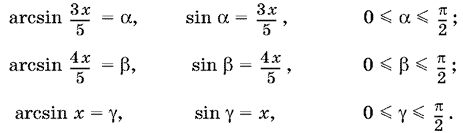
Перенеся ? в правую часть уравнения, получим ? = ? ? ?, причем 0 ? ? ? ?/2 и ??/2 ? ? ? ? ? ?/2. Поскольку обе части уравнения находятся в интервале монотонности синуса, то данное уравнение равносильно такому:
sin ? = sin (? ? ?).
Последнее уравнение можно записать в виде
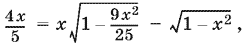
добавив к нему условие |4x/5| ? 1, являющееся в данном случае следствием уравнения. Получаем x1 = 0.
Остается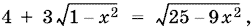 
а после возведения в квадрат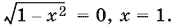 
Делаем проверку иррационального уравнения.
Ответ. ±1, 0.
22.10. Из условия следует, что x > 0. В таком случае
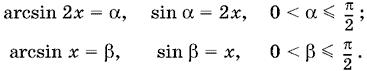
Уравнение примет вид ? + ? = ?/3, и обе его части окажутся в интервале (0, ?], который является интервалом монотонности косинуса. Следовательно, уравнение
cos (? + ?) = cos ?/3
равносильно данному. Раскрывая скобки и заменяя тригонометрические функции ? и ? их выражениями через x, придем к уравнению
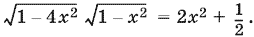
После возведения в квадрат получим
4(1 ? 4x?)(1 ? x?) = (4x? + 1)?.
При переходе к последнему уравнению могут появиться посторонние корни из?за того, что обе левые скобки могут стать отрицательными. Чтобы избежать этого, добавим условие |2x| ? 1.
Уравнение 28х? ? 3 = 0, к которому сводится последнее, имеет корни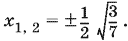 
Из них следует выбрать первый, так как он положителен и так как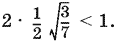 
Ответ.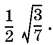 
22.11. Обозначим
arctg (2 + cos x) = ?, arctg (2 cos? x/2) = ?.
Так как 2 + cos x > 0 и 2 cos? x/2 > 0, то 0 < ? < ?/2 и 0 ? ? < ?/2.
Уравнение принимает вид ? ? ? = ?/4, причем
??/2 < ? ? ? < ?/2 и ??/2 < ?/4 < ?/2.
Так как (??/2, ?/2) — интервал монотонности тангенса, то уравнение ? ? ? = ?/4 равносильно уравнению tg (? ? ?) = tg ?/4.
Переходя к уравнению
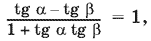
мы можем потерять те корни, для которых tg ? или tg ? не существует. В нашем случае этого не произойдет, поскольку
tg ? = 2 + cos x, tg ? = 2 cos? x/2,
а правые части существуют всегда. Получаем уравнение
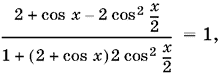
которое после преобразований принимает вид
2 cos4 x/2 + cos? x/2 = 0.
Так как уравнение 2 cos? x + 1 = 0 не имеет решений, то остается cos x = 0.
Ответ. ?(2n + 1).
22.12. Пусть
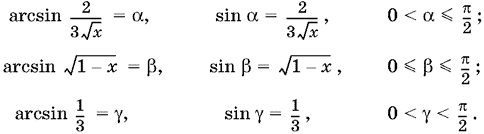
Так как ??/2 < ? ? ? ? ?/2, то обе части уравнения лежат в интервале монотонности синуса. Поэтому уравнение равносильно такому:
sin (? ? ?) = sin ?
или
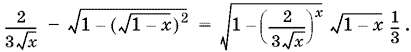
После упрощений получим уравнение
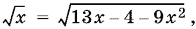
имеющее единственный корень x = ?. Делаем проверку и убеждаемся, что x = ? является корнем предыдущего уравнения и, следовательно, корнем исходного уравнения.
Ответ. ?.
22.13. Введем обозначения
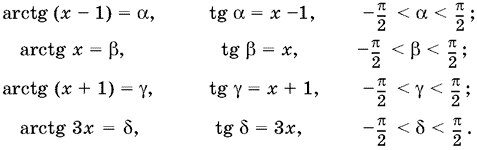
Наше уравнение принимает вид ? + ? + ? = ? или ? + ? = ? ? ?. Обе части уравнения лежат в интервале (??, ?). Если мы возьмем котангенсы от обеих частей уравнения, то можем потерять лишь корень, которому соответствует значение углов, равное 0, так как это — единственное значение из интервала (??, ?), в котором котангенс не существует. Проверим, будет ли выполняться равенство ? + ? = ? ? ? = 0. Если ? + ? = 0, то arctg (1 ? x) = arctg x, откуда 1 ? x = x и x = ?. При x = 1 получим, что ? ? ? = arctg 3/2 ? arctg 3/2 = 0. Таким образом, x1 = ? — корень уравнения. Если ? + ? ? 0, то от обеих частей уравнения можно взять котангенсы:
ctg (? + ?) = ctg (? ? ?),
что приведет к следствию исходного уравнения. Раскрыв скобки и подставив выражения тригонометрических функций ?, ?, ? и ? через x, получим уравнение
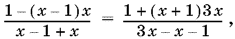
которое равносильно системе
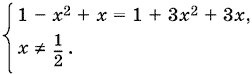
Получаем два значения неизвестного: x2 = 0, x3 = ??. Проверкой убеждаемся, что оба значения удовлетворяют данному уравнению.
Ответ. 0, ±?.
Больше книг — больше знаний!
Заберите 20% скидку на все книги Литрес с нашим промокодом
ПОЛУЧИТЬ СКИДКУ