K главе 15
15.1. В правой части можно произвести логарифмирование, не нарушая равносильности.
15.2. Рассмотреть случаи 0 < tg x < 1 и tg x > 1. Удобно выразить sin? x через tg? x. (!)
15.3. Нетрудно заметить, что на самом деле интервал можно сузить: 0 < x < ?/2 , так как при ?/2 < x < ? функции, стоящие под знаком логарифма, отрицательны.
15.4. Вначале нужно привести все логарифмы к общему основанию с помощью формулы logak N = 1/k loga N.
15.5. Неравенство эквивалентно условию, что основание логарифмов лежит между 0 и 1.
15.6. Начать следует с приведения левой части к виду, удобному для логарифмирования. Это позволит перейти к неравенствам, где уже не будут участвовать тригонометрические функции.
15.7. Использовать тот факт, что arccos у ? 0. Чему равносильно данное в условии неравенство?
15.8. Область значений левой части неравенства — интервал от 0 до ?/2 , а область значений правой части — интервал от 0 до ?. Так как левая часть должна быть больше правой, то аргумент арккосинуса не может стать отрицательным.
15.9. Второй сомножитель неотрицателен при всех x, следовательно, неравенство может удовлетворяться лишь при положительных значениях первого сомножителя. Если произведение двух положительных чисел не меньше единицы, то хотя бы одно из них не меньше единицы.
15.10. Обозначим первый сомножитель через А, а второй через В. Так как А ? 0, то неравенство равносильно совокупности двух систем:
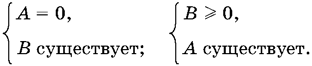
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК