Всегда ли площадь линии равна нулю?

Конечно, после того как читатель познакомился с линиями, проходящими через все точки квадрата, он может ожидать чего угодно. Но все же, может ли линия иметь площадь? Ведь еще Евклид говорил, что линия — это длина без ширины. А там, где нет ширины, нет, казалось бы, и площади. Да и в определении канторовой линии сказано, что она не содержит ни одного целого куска плоскости. Откуда же в этом случае взяться площади? Но мы уже много раз видели, что применение бесконечных процессов приводит к совсем неожиданным результатам.

Прежде чем исследовать вопрос, надо договориться о точном смысле употребляемых слов. Что значат слова "линия имеет нулевую площадь" или "линия имеет ненулевую площадь"? Возьмем самую обычную линию — прямолинейный отрезок. Так как его ширина равна нулю, то отрезок можно поместить внутрь прямоугольника сколь угодно малой площади, нужно лишь выбрать ширину этого прямоугольника достаточно малой. Точно так же и окружность можно поместить внутрь многоугольника со сколь угодно малой площадью. Для этого достаточно вписать в нее правильный многоугольник с очень большим числом сторон и описать аналогичный многоугольник. Область, заключенная между этими двумя многоугольниками, будет иметь малую площадь (тем меньшую, чем больше сторон у наших многоугольников), а окружность целиком лежит в этой области (рис. 27).

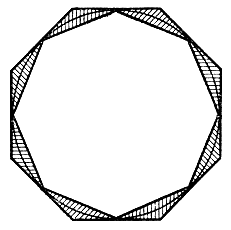
Рис. 27

Теперь уже ясно, что означают слова линия имеет нулевую площадь. Они значат, что, какое бы маленькое положительное число ? мы ни взяли, найдется многоугольная область, содержащая линию и такая, что площадь области меньше, чем ?. А если хоть для одного положительного ? такой области не удастся найти, тогда площадь линии не равна нулю.

Применим теперь это определение не к таким простым линиям, как отрезок или окружность, а к более сложным, например к ковру Серпинского. Простой подсчет показывает, что после n выбрасываний остается фигура, площадь которой равна (⁸/₉)ⁿ. Но ⁸/₉ — правильная дробь, а при возведении такой дроби в степень с увеличением показателя результат уменьшается и стремится к нулю. Это означает, что для любого ?>0 после достаточно большого числа шагов получится многоугольная область, площадь которой меньше, чем ?. А эта область целиком накрывает ковер Серпинского. Выходит, площадь ковра Серпинского равна нулю.

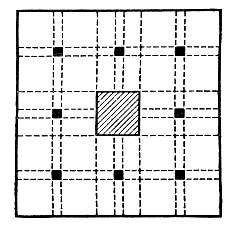
Рис. 28

Казалось бы, полный триумф определения Евклида. Даже у такой сложной линии, как ковер Серпинского, площадь равна нулю. Но праздновать победу преждевременно. Ведь никто не заставлял нас выбрасывать такие большие куски. На рис. 28 изображен более экономный способ выбрасывания квадратиков. Подбирая должным образом их размеры, можно добиться того, чтобы общая площадь выброшенных фигур не превышала ¹/₂. Но тогда на каждом шагу описанного процесса будет оставаться многоугольная область, площадь которой никак не меньше, чем ¹/₂. Отсюда легко следует, что остаток, получающийся после всех выбрасываний, не удастся покрыть многоугольной областью, если ее площадь окажется меньше, чем ¹/₂. Значит, о нем нельзя сказать, что его площадь равна нулю. А ведь этот остаток, как и ковер Серпинского, является кривой (в смысле Кантора) — при его построении мы дырявили каждый прямоугольник и ни одного целого прямоугольника не оставили.

Выходит, таким образом, что кривая в смысле Кантора может иметь ненулевую площадь!